前言

侧信道分析是一种新型的密码破解手段，其针对加密设备在运行过程中产生的时间消耗、功率消耗或电磁辐射等旁路信息进行分析达到攻击效果。侧信道攻击的有效性远高于密码分析的数学方法。该技术发展至今已经有了许多种实现，如时序攻击、能耗攻击、电磁攻击等，对常见的加密算法如 AES 、 DES 、 RSA 和 ECC 都有对应的攻击手段。与传统密码分析学相比，侧信道攻击显著的攻击效果使其作为一种新的密码分析方法迅速称为研究的热点。而本文围绕时序攻击这个主题，用比较简单基础的例子来介绍这一种攻击手法（其实就是我本身水平也不高XD

正文

在密码学中,时序攻击是一种侧信道攻击,攻击者试图通过分析加密算法的时间执行来推导出密码。每一个逻辑运算在计算机需要时间来执行,根据输入不同,精确测量执行时间,根据执行时间反推出密码。（来自百度百科）

实际上这种攻击手段和 SQL 注入中的时间盲注是类似的，都是利用“时间”这种旁路信息来判断程序内部的运行状态从而进行推导，最终获取目标信息。

Password恢复

假设一个比较经典的场景，某个系统通过一个 strcmp 函数对用户输入的 password 和系统中内置的密码进行比较，一致就能登入系统。这里的 strcmp 实现如下：

int strcmp(const char *s1, const char *s2) {
 for ( ; *s1 == *s2; s1++, s2++) 
if (*s1 == '\0')
 return 0;
 return ((*(unsigned char *)s1 < *(unsigned char *)s2) ? -1 : +1);
 }

这就是C语言本身 strcmp 的实现，思路比较简单：就是给定的两个串逐位比较，遇到不相同的就直接返回。

按照这种实现，我们用极限的思维去思考，假设我们系统设置的密码是 'a'*∞ ，当我们输入 abbbbbbb.. 时函数会很快返回，但是输入 'a'*∞ 时函数内部则会一直逐位比较。也就是说这两种输入的比较次数不同，那么最直观的体现就是时间，前者很快就返回，后者则会无穷等待。

假设比较一次消耗的时间单位是 1t 且固定不变，那么不难得出 strcmp("123","000") 和 strcmp("123","100") 的执行时间分别是 1t 和 2t 。我们的攻击思路也就非常清晰了。

接下来进行模拟。由于现代的计算机算力非常发达，这种逐位对比的时间消耗差异是很微妙的，即使是现实中的一些算力比较低的设备也需要比较精准的仪器才能测量内部的差异。所以为了降低误差，我们需要对 strcmp 进行小改。改动后的函数实现如下：

int new_strcmp(const char*s1, const char*s2){
for(;*s1==*s2;s1++,s2++,usleep(5000)) // 如果字符相同，增加一定的延时。
if(*s1=='\0')
return 0;
return ((*(unsigned char *)s1<*(unsigned char *)s2)?-1:+1);
}

通过以上改动，字符判断相同的情况和不同的情况就会出现一个 5ms 的差异。但是需要注意的一点是，延时 5ms 是为了使模拟攻击更容易实现而人为添加的，实际的攻击中我们一开始是不知道这个差异时间是多少，这一点与SQL注入中的时间盲注是不一样的。所以我们需要进行简单的测试来得到这个差异。

#include<stdio.h>
#include<time.h>
int new_strcmp(const char*s1, const char*s2) {
for(; *s1==*s2; s1++,s2++,usleep(5000))
if(*s1=='\0')
return 0;
return ((*(unsigned char *)s1<*(unsigned char *)s2)?-1:+1);
}
clock_t start, end;
unsigned char password[] = "admin888"; // 设定密码是admin888
int main() {
unsigned char guess_char = 0;
unsigned char leak_str[16] = {0};
for(guess_char = 1; guess_char!=0; guess_char++) {
leak_str[0] = guess_char;
start = clock();
new_strcmp(password,leak_str);
end = clock();
printf("[*] Guess ascii 0x%02X, time：%lf\n", guess_char, (double)(end-start)/CLK_TCK);
}
return 0;
}

其实就是通过对第一位进行猜解，可以得到一些数据样本：

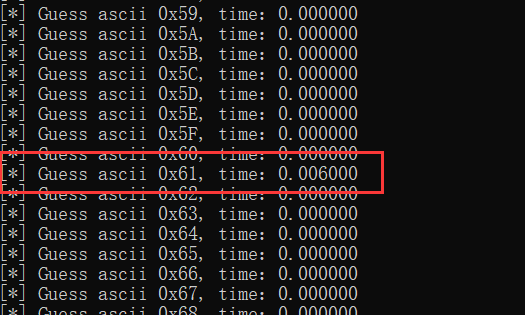
这里模拟攻击的时间差异是非常明显的，当猜对时函数执行时间比猜错多了 0.006s 而且也是比较稳定的。但是在真实的攻击中往往需要多次测试获取更多的样本进行分析计算才能得出一个比较稳定的差异值。利用这个差异我们就可以判断出相应位的字符是否正确，就通过可以逐位猜解获得目标字符串。
这里直接贴出代码：

#include<stdio.h>
#include<time.h>
int new_strcmp(const char*s1, const char*s2) {
for(; *s1==*s2; s1++,s2++,usleep(5000))
if(*s1=='\0')
return 0;
return ((*(unsigned char *)s1<*(unsigned char *)s2)?-1:+1);
}
clock_t start, end;
unsigned char password[] = "admin888";
int main() {
int bool_end_flag = 1, leak_str_index = 0;
double strcmp_time = 0.0, diff_time = 0.0;
unsigned char guess_char = 0;
unsigned char leak_str[16] = {0};
while(bool_end_flag) {
bool_end_flag = 0;
for(guess_char = 1; guess_char != 0 ; guess_char++) {
// 遍历0x01-0xFF字节，这里的坑是如果guess_char类型为char则不能用<=0xFF判断，会溢出为0造成死循环。
// 如果能确定密文空间那只需要遍历密文空间即可。
leak_str[leak_str_index] = guess_char;
start = clock();
new_strcmp(password, leak_str);
end = clock();
diff_time = (double)(end-start)/CLK_TCK - strcmp_time; // clock_t 计数，精确到微秒。
if(0.004 < diff_time && diff_time < 0.008) { // 给 6ms 一个 2ms 的浮动范围。
printf("Hint byte:'%c', Leak out:%s\n", guess_char, leak_str);
bool_end_flag = 1;
strcmp_time = (double)(end-start)/CLK_TCK;
break;
}
}
leak_str_index++;
}
return 0;
}

运行效果如图：

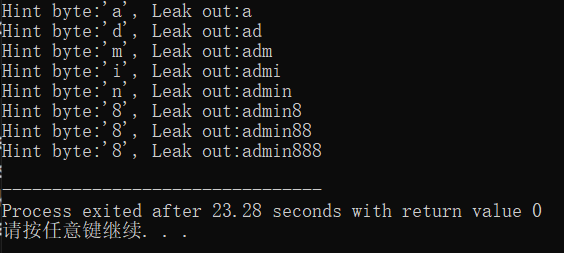
可以看到成功 leak 出了内置的密码，但是由于是模拟攻击，还是比较理想化的。在真实的攻击中往往还存在许多影响因素，所以往往需要多次采样，分析，剔除影响因素。
这里抛出问题：采集时间差异是必要的吗？直接取耗时最高的是否可行？

GF(2^8)有限域乘法的时序攻击

有限域乘法通俗的说就是运算结果都在一个域中，在密码学中很常用，例如AES用到的就是GF(2^8)有限域乘法。这里也不讲其原理，直接给出实现算法。

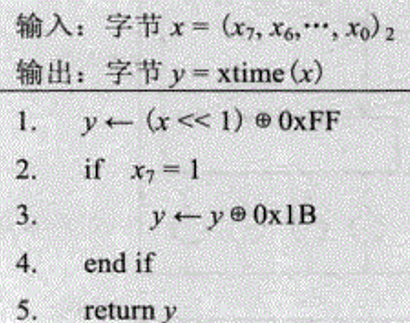
用C语言实现

unsigned char xtime(unsigned char x) {
unsigned char y;
y = x<<1;
if(x&0x80) {
y^=0x1B;
}
return y;
}

简单的解释就是，输入字节 x 会先左移1位，如果原字节x的最高位 x7 为1，那么还会再异或 0x1B 。也就是说 x7=0 时 x 会被处理1次，而 x7=1 时会被处理2次，这也就出现了差异，我们可以知道这个操作次数的差异是可以在时间上体现出来的。

那么我们先基于这个有限域乘法实现一个加密算法。

unsigned char encode(unsigned char a) {
unsigned char k=0xAE, x, y; // k为加密密钥
x = a ^ k;
x = S_Box[(x>>4)&0xf][x&0xf];  // AES算法中的S盒
y = xtime(x);
return y;
}

我们假设这个算法流程是公开的，其中的 xtime 和 S盒 都是公开已知的，而k值就是由使用者给出，我们攻击者的目标就是获取k的值。

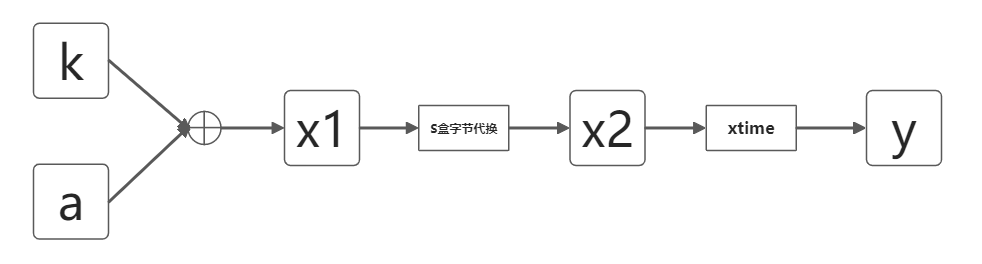
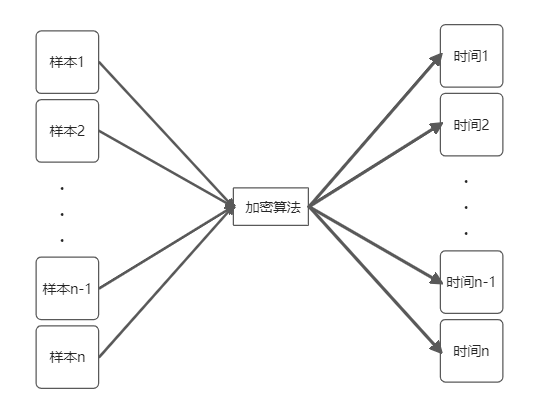
以上画出一个简单的图，我们不难知道xtime的参数 x2 是和 xor(a,k) 相关的。同时 a 是我们可控的，且算法流程也知道，基于这点我们就可以利用时间差分来攻击这个加密算法。

还是一样，我们先进行比较理想的设定，把操作一次的时间设定为 1t 且不变, 那么 xtime 算法根据输入的不同就会出现执行时间为 1t 和 2t 两种情况。

我们的攻击思路如下：

首先准备一定数量的随机样本，然后喂给加密算法，并记录每个样本对应的加密时间。

根据之前的设定，统计结果可以按加密时间分为两组，一组为 1t 另一组为 2t （通俗的说就是一部分加密时间比较短，另一部分加密时间相对较长）。得到这些分组的统计数据后，计算两组的平均时间->作差->求绝对值，结果不难得到是 1t 。

由于k值的范围在0x00-0xFF，所以我们可以通过模拟这个加密算法，用不同的k值去加密相同的样本，同时和前面一样记录每个样本的加密时间。同样进行分组，但是这次的分组是按照前面的分组进行分组（稍微理解一下），也就是说，对于某个样本以及某个猜测的k值，不管其加密时间是长还是短，都按照被攻击的k值的分组情况进行分组。分组完成后，同样计算两组的平均时间->作差->求绝对值。

直接举例子：

首先用k（未知）加密一些样本。假如统计的情况如下：
s1 = 1t
s2 = 1t
s3 = 2t
s4 = 1t
也就是
Group1 : [s1,s2,s4]
Group2 : [s3]
接下来通过模拟加密算法去猜k值。
假如k1的加密时间统计情况是：
s1' = 2t
s2' = 2t
s3' = 2t
s4' = 1t
那么按照Group1和Group2的分组，计算其平均时间分别得到
(s1'+s2'+s4')/3 = 5/3t = 1.66t
s3'/1 = 2t
作差再求绝对值得到0.34t
假如k2的加密时间统计情况是：
s1'' = 1t
s2'' = 1t
s3'' = 2t
s4'' = 1t
(s1''+s2''+s4'')/3 = 3/3t = 1t
s3''/1 = 2t
作差再求绝对值得到1t
那么这时，k2和k就表现出了相关性，当样本足够多时就可以认为这个相关性是很强的，那么k2就是我们要找的k了。

下面进行编码模拟攻击，首先需要小改一下xtime函数

unsigned char xtime(unsigned char x) {
unsigned char y;
y = x<<1;
if(x&0x80) {
y^=0x1B;
usleep(10000); // 增加10ms的延时
}
return y;
}

完整代码：

#include<stdio.h>
#include<time.h>
#include<math.h>
static const unsigned char S_Box[16][16] = {...}; // AES的S盒，随便上网抄一个即可。
unsigned char xtime(unsigned char x) {
unsigned char y;
y = x<<1;
if(x&0x80) {
y^=0x1B;
usleep(10000);
}
return y;
}
// 被攻击的函数，其中k是我们要获取的。
unsigned char encode(unsigned char a) {
unsigned char k=0xAE, x, y; 
x = a ^ k;
x = S_Box[(x>>4)&0xf][x&0xf];
y = xtime(x);
return y;
}
// 模拟加密函数
unsigned char guess_encode(unsigned char a, unsigned char k) {
unsigned char x, y;
x = a ^ k;
x = S_Box[(x>>4)&0xf][x&0xf];
y = xtime(x);
return 0;
}
clock_t start, end;
double run_time;
int main() {
double delay_group_time_sum = 0.0, nodelay_group_time_sum = 0.0;
int i = 0, guess_k = 0;
int sample_num = 0x10, delay_cnt = 0, nodelay_cnt = 0, bool_delay_group[0xFF] = {0};
unsigned char sample = 0x00;、
// 喂样本操作，这里的样本是0,1,..,15
for(sample=0; sample<sample_num; sample++) {
start = clock();
encode(sample);
end = clock();
run_time = (double)(end-start)/CLK_TCK;
// 判断是否有延时，也就是按时间长短分组。
if((int)(run_time/0.01)==1) {
bool_delay_group[sample] = 1; // 用1标注该样本是2t的组。
delay_cnt++; // 统计个数，用于求平均值。
} else {
// 同上
bool_delay_group[sample] = 0;
nodelay_cnt++;
}
}
// 猜测k值
for(guess_k=0; guess_k<=0xFF; guess_k++) {
// 加密相同的样本
for(sample=0, delay_group_time_sum=0.0, nodelay_group_time_sum=0.0; sample<sample_num; sample++) {
start = clock();
guess_encode(sample, guess_k);
end = clock();
run_time = (double)(end-start)/CLK_TCK;
// 根据前面的分组，求时间总数
if(bool_delay_group[sample])delay_group_time_sum+=run_time;
else nodelay_group_time_sum+=run_time;
} 
// 平均->作差->绝对值
printf("0x%02X, %lf\n", guess_k, fabs(delay_group_time_sum/delay_cnt - nodelay_group_time_sum/nodelay_cnt));
}
return 0;
}

编译运行：

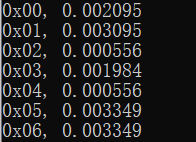
可以看到一些猜错的k值因为错误的分组所以差分后相关性比较弱。

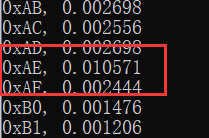
而猜对的时候由于分组完全符合，就可以计算出我们设定的10ms的差异结果，也就是说分组的相关性很强，这样就可以得到k值为 0xAE 了。

收尾

侧信道分析相比传统的密码分析学来说，它是一种比较旁门的手段，甚至可以说是猥琐。但是在安全攻防中，手段并没有什么高低贵贱之分，总会有些人为了达到目的用尽各种意想不到的手段。而安全的本质就是对风险和异常的管理，一切都应防范于未然，所以无论是侧信道还是什么偏门且猥琐的手段，都有其研究的价值和意义。不管是进攻还是防守，只有知己知彼才能百战百胜。