0x01 序言

这几年人工智能、大数据技术的快速发展创造了很多机会和应用，但也使得人们的隐私数据正在不断的被各种技术平台、厂商收集。这些平台、厂商为了追求商业利益或提升技术水平，总是会主动或被动的将用户的隐私数据用于自己使用或卖给其它公司进行人工智能或大数据分析。这在一定程度上侵害了用户的个人隐私。

为了保护个人隐私，欧盟在 2018 年正式实施了《通用数据保护条例》（General Data protection Regulation, GDPR），随后在全世界范围内都陆续有隐私保护的相关法律法规出台，我们国家就个人隐私提出了《个人信息安全规范》等保护条例。鉴于个人和政府对隐私的重视，很多厂商加强了对大数据中的个人隐私保护力度，比如数据匿名化技术。数据匿名化通过抑制、泛化、聚合等手段来将发布的数据集中的敏感信息隐藏，这在一定程度上能够保护用户的个人隐私。但如果要防范一些专业的隐私窃取组织则远远不够。

现在考虑这么一种隐私窃取模型，设想一个受信任的机构持有涉及众多人的敏感个人信息（例如医疗记录、观看记录或电子邮件统计）的数据库，且能够提供一个全局性的统计数据。这样的系统被称为统计数据库。尽管表面看来，只有经过处理的统计特征被发布，但这些统计结果也有可能揭示一些涉及个人的信息。例如，当研究人员同时使用两个或多个分别进行过匿名化处理的数据库时，个人信息的匿名化手段仍然可能失效。比如：现有一个仅能查询全局性统计数据的查询人员，他首先查询了某科室今日接诊的100个人中，有5个是患艾滋病的，现在查询人员修改了查询条件，将张三从这100个人中剔除（比如张三的数据被手动标记了重复）重新再查询，发现有4个患艾滋病。那么此时查询人员可以推测，张三患艾滋病。上述的攻击技术主要是通过对统计数据库的查询结果和查询条件进行分析，我们称这类技术为统计数据库再识别技术。

差分隐私就是为防护这类统计数据库再识别技术而提出的一个概念。差分隐私技术的引入一方面可以使得企业能够在不侵犯个人隐私的情况下，使用大量的敏感数据进行研究或商业化用途。另一方面，研究机构可以基于差分隐私来开发适合数据社区的敏感数据云共享技术，在不侵犯个人隐私的情况下，解决数据共享的问题。

0x02 差分隐私介绍

2.1 差分隐私的基本概念

差分隐私（Differential privacy，简称 DP) 是在统计学和机器学习分析背景下的关于隐私的一个强数学定义。目的是使得数据库查询结果对于数据集中单个记录的变化不敏感。换句话说，就是某个记录在不在数据集中对最终的查询结果的影响是非常小的。这样就可以防止某些攻击者通过增加或删除数据集中的某条记录，进而根据所得的查询结果来进行差分分析来提取隐私。差分隐私中的差分主要就体现在查询结果的差分中。如图1所示。

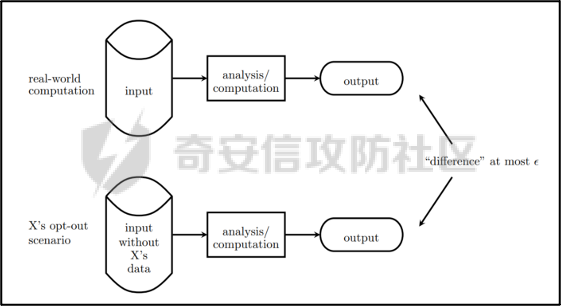
图1差分隐私基本概念

2.2 差分隐私实现思想

前文提到差分隐私主要是为了使得数据库查询结果对于数据集中单个记录的变化不敏感。也就是说要对查询结果进行一定的调整。使得单个记录的变化在查询结果上是体现不出来的。为了达到这样的效果，差分隐私的做法是给查询结果增加一定的随机噪声。比如刚才的医疗科室查询案例，增加随机噪声以后，可能100个接诊病人中，查询到的是5人患癌症，此时的噪声是0，而剔除张三再查询，查询到的还是5人，此时噪声是+1。而对于攻击者来说，是没有办法确定噪声是多少的。所以无法判断张三是否患癌。但是这样就新的问题了，加了随机噪声以后，查询到的数据已经不再精准了，那么数据本身的价值就降低了。这的确是差分隐私需要考虑的现实问题。那么差分隐私是怎么解决的呢，一方面，差分隐私通过更准确的概率模型来尽可能的让查询结果精准。另一方面，差分隐私提供了隐私预算 ε 来量化隐私保护级别。 ε 的值越低，则隐私保护的越好，但也会导致数据的准确度越低。所以具体设置怎样的隐私保护级别，需要开发者自行权衡。为了更好的展示差分隐私的能力，在此举一个经典的例子。

**案例**1**：**某社会调查为了统计社区内家庭中男性出轨的比例，最开始想到的是问卷调查的方式，但是发现这样会侵犯到被调查者的隐私。于是利用差分隐私技术，对调查结果增加噪声，采用抛硬币统计法。具体的做法如图2-1所示。被调查的个体在回答问题之前，首先抛一枚硬币，如果正面朝上，则如实回答。如果正面朝下，则再抛一次硬币，如果正面朝上，则回答“是”，正面朝下则回答“否”。

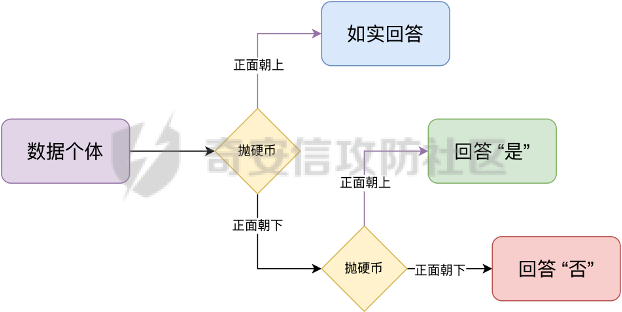
图 2-1 抛硬币统计方案

在这个统计方法中，不难发现任何一个个体都至少可能1/4的可能回答 “是”，因为抛硬币这个动作是随机的。所以尽管有个体回答了 “是”，也无法猜测该个体到底是不是真出轨了。这也就解决了隐私泄露的问题。既然隐私泄露问题已经解决，那么怎么得到较为准确的结果呢。则可以通过概率统计学的方法进行计算：假设共有N个数据个体，其中真正出轨的个体数量为M，经过抛硬币法统计后的回答 “是” 的个体共有T个。那么 T 的组成如下：

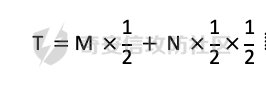
既然T和N是已知的，那么M也就能够计算出来的。当然，在这里我们假设了一次抛硬币正面朝上的概率是1/2，但实际上或许存在偏差。所以计算得到的M也会存在一定的偏差。不过这种偏差一般不大，这是能够接受的。

2.3 差分隐私数学定义

假设有随机算法M, S 是 M 所有可能输出结果组成的集合，Pr [·] 表示概率，对于任意两个相邻的数据集D和D’, D和D’之间只有1条记录是不一样的。如果能够满足：

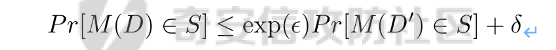
我们在此先只考虑 δ \= 0 的情况， δ \= 0 时称算法M提供是提供 ε-差分隐私保护（ε-differentially private)。其中 ε 也叫作差分隐私预算。现在对公式做一下简单的变换，将D好D’ 替换位置（D和D’ 只相差一个条记录，反过来一样是成立的）则有：

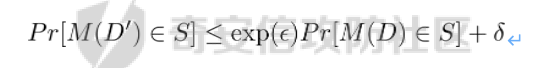
又因为 δ \= 0，则不难得出：

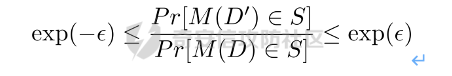
所以，ε 越接近于0，随机算法M在D和D’输出的数据分布越接近，它们表示的结果就越难区分，也就意味着隐私的保护程度越高。当 ε \= 0 时，M在D和D’在输出某个结果的概率就完全一样，输出结果不可区分。但此时原始数据的价值也就没了，因为根据公式继续推算的话，最后会发现M在相邻数据集中产生任意结果的概率是一样的，也就是说，M的结果完全独立于数据本身（完全随机）。所以无论是在人工智能还是大数据分析上，都需要数据分析者权衡 ε 的取值来兼顾隐私和数据价值。

2.4 拉普拉斯机制

在前面节介绍了差分隐私的数学定义，也知道了差分隐私主要通过增加噪声来缩小结果对单个记录改变的敏感度。但是噪声具体怎么增加？怎么去量化？这些问题并没有解决。要想让差分隐私真正可用，则必须有一个具体的机制来增加噪声，随后的研究中，人们发现拉普拉斯分布是能够满足 ε-差分隐私保护的，可以在数值型的数据库查询结果中加入服从拉普拉斯分布的噪声来实现差分隐私保护。拉普拉斯分布的概率密度函数为：

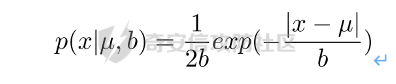
拉普拉斯产生的概率密度函数如图2-2 所示：

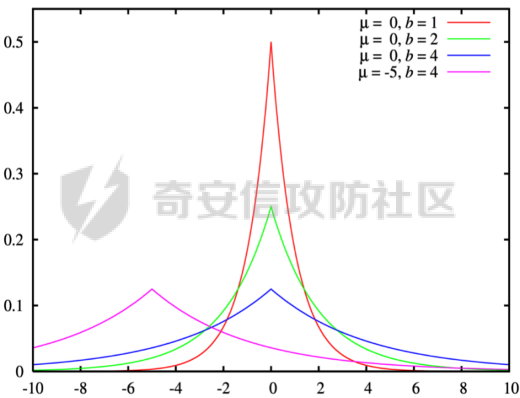
图 2-2 拉普拉斯概率密度函数

2.5 RNM

在文章 《The Algorithmic Foundations of Differential Privacy》 第35页通过一个例子解释 RNM 算法。

**案例****2 最常见的医学疾病：*假设我们希望知道哪一种疾病是在一组被调查者的医疗史中最常见，则需要进行一系列的调查。但是由于个人不希望别人知道其病史，所以需要在每个计数中添加 Lap*(1/ε) 噪声来解决。尽管通过噪声来保护个人的隐私，但是如果将所有的计数公布出去，尽管这些计数带了噪声，但还是会披露其它疾病的信息（我们需要统计的是最常见的，根据信息最小化原则，别的疾病信息不应该被披露）。所以需要使用RNM 报告最大的含有噪声的计数，而不是公布所有的计数结果。还有一点需要 指出的是，RNM 算法也是符合 ε-差分隐私保护的。

下篇

0x01 序言

前面在《差分隐私介绍与实践》的上篇中系统的介绍了差分隐私。那么在本篇章将主要讲讲差分隐私在深度学习方面的实践。

0x02 差分隐私保护实践

2.1 模型反转攻击

2015年，Matt Fredrikson 等学者提出了模型反转攻击[1]。该攻击方法主要利用机器学习模型的置信度来反推训练数据。作者通过实验证明，该攻击方法能够仅仅使用一个姓名就能够通过人脸预测模型还原训练时所使用的人脸图像。如图2-1所示，其中左边的图为模型反转攻击通过姓名还原的图，而右边则是模型训练时使用的图。通过对比不难发现，还原出来的图和训练时的用图具有很大的相似性。

图2-1 利用模型反转攻击还原图与训练时图的对比

上述攻击案例中。模型反转攻击利用的学习模型的置信度还原训练数据，在一定程度上就是利用了统计数据库再识别技术。换句话说，模型反转攻击通过置信度（学习模型的结果）对训练数据中单条记录的不同的敏感度来猜训练数据的特点。这表明在机器学习领域应用差分隐私保护是必要的。

2.2 差分隐私应用到机器学习的基本思想

差分隐私的基本思想是通过添加随机噪声来降低结果对训练数据引起的差分的敏感度。所以，在机器学习领域，差分隐私保护要求在加入随机性后，攻击者很难去区分在学习模型的最后产生的结果哪些是来自随机噪声，哪些是来自真正的训练数据。也就是说，需要做到当改变训练集中的单条训练样本，模型最终训练出来的结果（参数）是保持大致相同的。如图2-2所示，两个模型在存在一条训练样本差分的情况下，仍然可以通过随机函数产生相同的结果，那攻击者就无法通过结果反推训练样本的信息。

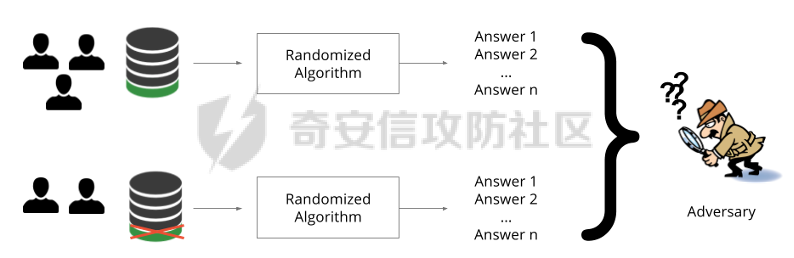
图2-2 差分隐私应用到机器学习基本思想

2.3 PATE

Google Brain 的研究团队，在2017年提出了PATE方案[2]，PATE( Private Aggregation of Teacher Ensembles) 翻译为教师综合下的隐私聚合，它通过差分隐私保护技术实现了在不暴露原始数据的前提下训练公共数据。PATE 基于一个简单的想法：如果两个独立的分类器（机器学习模型），双方在没有共同训练样本的不同数据集上训练，最终如果对一个新的输入样本达成了相同的分类结果，那么就不会泄露单个训练样本的信息。但是如果产生了不同的结果，那可能会暴露与输入样本记录相像的单个训练样本的信息。例如：假设张三患有癌症，并且张三只将病历信息贡献其中一个分类器。现有一个与张三病历相似的输入样本给到这两个学习模型预测，如果训练过张三样本的分类器返回了癌症的结果，而另外一个样本没有。那么很有可能返回癌症结果的分类器因为学习过张三的病历信息，所以产生了癌症结果。这样就暴露了张三患癌症的隐私。

那么，PATE是如何基于上述想法进行隐私机器学习的呢？具体步骤如下，其中步骤a-c 如图2-3所示，步骤d-f 如图2-4所示。

a. 将隐私数据集划分为N个数据子集。注意：这个N个数据集之间是没有重叠的样本的（为何这里需要不重叠数据集呢？不妨假设所有的教师都使用同一个数据集训练，那么所有的教师输出的结果将会是一样的。去除其中一个或多个教师多结果不会造成影响，这跟仅仅使用一个教师模型是一样的效果了，差分隐私起不到作用，因为分类器的结果将变得单一，增加噪声无任何意义。

b. 针对这个N个子集，分别使用N个称为“教师模型” 学习模型进行训练。

c. 等所有教师模型训练完成后，这N个教师模型就相当于有N个预测模型了。

此时，教师模型是没有差分隐私保护的，单个教师模型产生的预测结果可能会单个记录的隐私信息的影响。因此需要对教师模型的分类结果进行隐私聚合处理以保护隐私。具体步骤如下：

d. 统计所有教师的结果，并对统计结果增加符合高斯分布的噪声。

e. 使用RNM 算法返回投票值最高的标签。这个投票值是含有噪声的。

f. 最终输出聚合结果。

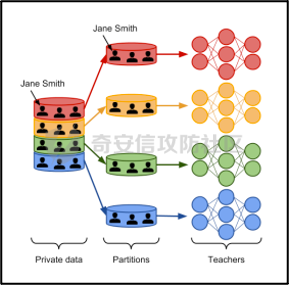
图2-3 教师模型训练过程

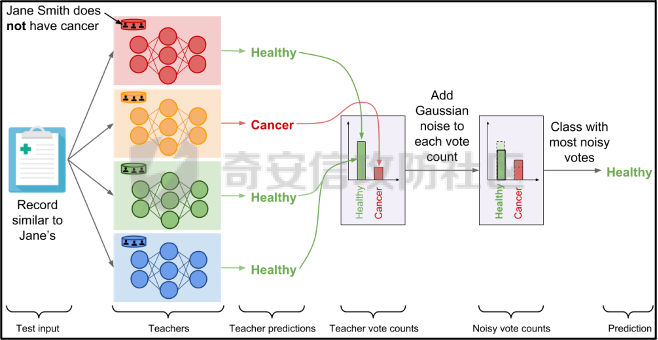
图 2-4 教师模型的隐私聚合过程

经过多个不同隐私数据训练的独立的教师模型的结果经过聚合以后，由于噪声的影响，其最终的输出结果将不再对单个训练样本的差分而敏感。但是这里面仍然存在一些受限的地方，主要有以下两个制约：

1. 每一次教师模型的预测，都将增大隐私预算

2. 教师模型的中间过程必须是保密的，一旦中间过程泄露，那么恶意攻击者将直接获取到单个教师模型的输出，那么差分隐私保护就失效了。

针对上述问题，PATE引入了学生模型。学生模型通过迁移教师模型的知识来完成训练。对于公开的数据但无标签的数据集，可以通过调用PATE中教师模型的隐私聚合查询API获得预测值，从而变成有标签的数据集，然后学生模型使用这些数据进行训练。

2.4 对PATE模型的隐私损失的分析

PySyft 是在Github 上开源的，用于在深度学习框架中保护训练集隐私的工具集。主要通过联邦学习、差分隐私保护和加密计算（比如多方安全计算和同态加密）等技术来保护隐私。本节将使用PySyft 中集成的PATE分析工具来估算在使用了PATE框架以后的隐私损失情况。PySyft 的pate工具中的perform_analysis 方法会给出两个值，分别是Data Dependent Epsilon 和 Data Independent Epsilon，Data Dependent Epsilon 意味着结合数据本身和当前差分隐私 ε 取值来看，隐私损失的情况，而Data Independent Epsilon 抛开数据本身，仅分析差分隐私 ε 取值所对应的隐私损失。

所以首先需要安装 PySyft，PySyft的安装非常方便，直接使用pip install syft安装即可，这里建议安装0.2.9版本，太新的版本在结构上有所改动。为了方便演示以及后期读者的复现，我在此使用Google Colab 在线平台进行实验。具体步骤如下：

1. 首先进入到 Google Colab 平台，新建笔记本。

2. Google Colab 使用了jupyter notebook 那一套框架，所以可以在上面执行python代码，首先安装依赖，输入命令：!pip install syft==0.2.9 平台会给我们分配资源并且进行依赖安装，安装完成后需要点击重启notebook按钮。如下图2-5所示

图2-5 环境安装

3. 导入所需要的依赖包，主要是pate分析工具和numpy（numpy用于生成模拟数据），执行命令：import numpy as np 和from syft.frameworks.torch.dp import pate

4. 定义RNM方法，代码如下：

defcal\_max(teacher\_preds,num\_labels):
indices = \[\]
foriinrange(teacher\_preds.shape\[1\]):
label\_counts = np.bincount(teacher\_preds\[:,i\], minlength=num\_labels)
max\_label = np.argmax(label\_counts)
indices.append(max\_label)
returnnp.array(indices)
defnoisy\_max(teacher\_preds,privacy\_loss\_lv,n\_labels):
indices = \[\]
foriinrange(teacher\_preds.shape\[1\]):
label\_counts = np.bincount(teacher\_preds\[:,i\], minlength=n\_labels)
noisy\_counts = label\_counts + np.random.laplace(np.zeros(len(label\_counts)), np.ones(len(label\_counts))/privacy\_loss\_lv,len(label\_counts))
indices.append(np.argmax(noisy\_counts))
returnnp.array(indices)

5. 开始实验，整个实验的思路如下：实验会通过四个实例来加深对PATE的理解，前三个实例为了让教师模型的聚合结果尽可能的接近原始数据本身，所以使用了较大的隐私等级 ε，因为 ε 越大，隐私保护程度越低，数据越接近与原始数据。具体步骤如下：

**实例****1**，假设教师模型数量为100个，测试样例1000个，所有的教师模型的输出都0。竟然所有的输出都为0，也就是说这里面不存在输出结果的差分，所以我们可以预计这里面是没有隐私信息泄露的。

使用numpy构造数据，并通过PySyft 的pate工具分析，执行下列代码：

num\_teachers, num\_examples, num\_possible\_answers = (1000,1000,1)
preds = np.zeros((num\_teachers, num\_examples, )).astype(int)
indices = cal\_max(preds, num\_possible\_answers)
data\_dep\_eps, data\_ind\_eps = pate.perform\_analysis(teacher\_preds=preds, indices=indices, noise\_eps=5, delta=1e-5, moments=70)
print("Data Independent Epsilon:", data\_ind\_eps)
print("Data Dependent Epsilon:", data\_dep\_eps)

最后得到的输出与我们预想的一样。如图2-6所示，其中Data Dependent Epsilon 的值非常低，而Data Independent Epsilon 比较高，这是因为所有教师模型的输出都为0，结果一样。也就是说无论怎么改变单个输入样本，结果都不会变。所以结合数据本身来看是没什么隐私泄露的，而由于我们的 ε 取值太高，所以抛开数据本身，是存在隐私泄露风险的。

图2-6 实例1的pate分析结果

**实例****2**，假设教师模型100个，测试样例1000个，每一个教师模型的输出都是从0-999。具体如图2-7所示。和实例1不同的是，现在不同的输入样本会产生不同的值，但是由于所有教师模型对每一个测试样例输出的结果都是一样的，去除其中一个或多个教师模型，并不会影响最终的结果。所以也不会有隐私信息的泄露。

图2-7 实例2的教师模型输出

使用numpy生成数据，执行pate分析，执行下列代码：

num\_teachers, num\_examples, num\_possible\_answers = (100,1000,1000)
preds = np.zeros((num\_teachers, num\_examples, )).astype(int) + np.expand\_dims(np.array(list(range(num\_examples))),0)
indices = cal\_max(preds, num\_possible\_answers)
data\_dep\_eps, data\_ind\_eps = pate.perform\_analysis(teacher\_preds=preds, indices=indices, noise\_eps=5, delta=1e-5, moments=70)
print("Data Independent Epsilon:", data\_ind\_eps)
print("Data Dependent Epsilon:", data\_dep\_eps)

图2-8 实例2的pate分析结果

最后得到的输出不出所料。如图2-8所示，其中Data Dependent Epsilon 的值非常低，说明结合数据来看，隐私损失很小。

**实例****3**，假设教师模型100个，测试样例1000个，每一个教师模型的输出都是随机生成的，区间范围为0-99。具体如图2-9所示。和实例2不同都是，实例3中每一个教师模型对每个测试样例的输出结果不再完全相同。现在假设去掉其中一个或多个教师模型，那可能会导致最终结果的不同。所以此时将存在隐私泄露的风险。

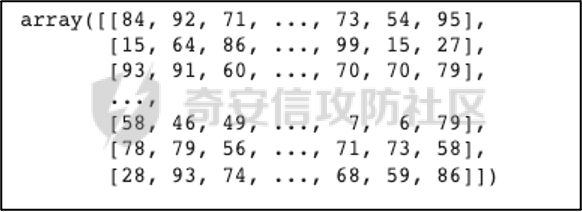
图2-9 实例3教师模型的输出结果

使用numpy生成数据，执行pate分析，执行下列代码：

num\_teachers, num\_examples, num\_possible\_answers = (100,1000,100)
preds = np.random.randint(low=0, high=num\_possible\_answers, size=(num\_teachers, num\_examples)).astype(int)
indices = cal\_max(preds, num\_possible\_answers)
data\_dep\_eps, data\_ind\_eps = pate.perform\_analysis(teacher\_preds=preds, indices=indices, noise\_eps=5, delta=1e-5, moments=70)
print("Data Independent Epsilon:", data\_ind\_eps)
print("Data Dependent Epsilon:", data\_dep\_eps)

最后得到的输出证明了前面的想法。如图2-10所示，其中Data Dependent Epsilon 和Data Independent Epsilon 都较高。这意味着的确存在泄露隐私的风险。

图2-10 实例3的pate分析结果

**实例****4**，实例3通过数据证明了在 ε 设置较高的情况下是存在隐私泄露风险的，所以在实例4需要将 ε 降低来验证差分隐私的确能够起到保护隐私的作用。还是使用同样的数据集，只是在pate分析时把noisy_eps 参数由原先的5，调到了0.0001。执行下列代码：

data\_dep\_eps, data\_ind\_eps = pate.perform\_analysis(teacher\_preds=preds, indices=indices, noise\_eps=0.0001, delta=1e-5, moments=70)
print("Data Independent Epsilon:", data\_ind\_eps)
print("Data Dependent Epsilon:", data\_dep\_eps)

最后得到的输出证明了差分隐私的有效性，在调低了 ε 以后，Data Dependent Epsilon 和Data Independent Epsilon 都降了下来。如图2-11所示。

图2-11 实例4的pate分析结果

通过上述四个实例，我们已经对PATE模型有了基本的了解了，PATE的核心就是将敏感的数据集拆分成多份，然后分别进入到独立的教师模型中训练，最后得到这些教师模型的学习参数。针对每一个教师模型产生的预测结果是不会单独公开的，必须通过增加噪声以后，通过RNM算法输出得票最高的结果。

2.5 PATE实践

前文已经对差分隐私保护做了详细的介绍。那么本节将通过一个深度学习实例来展开对PATE的实践。该案例就是深度学习中最常用的例子——手写数字的识别，训练和测试使用的数据则来自MNIST数据集。本节将MNIST数据集中部分数据当做敏感数据处理，将这部分敏感数据使用PATE中的教师模型去训练。而剩余的数据则当做公开数据，部分公开数据当成是没有标签的数据，让教师模型给出他们的隐私聚合后的预测值，再将预测值当成是这部分数据的标签。进一步的通过学生模型去训练这些数据，最终产生迁移了教师模型（敏感数据）知识的新模型。本案例同样在Google Colab 跑实验。由于篇幅关系，本节仅针对关键代码做解读，完整代码请直接参考附件1。下面对部分关键做解释：

1. 导入依赖包。

2. 下载并转换MNIST数据集，定义数据加载器。

3. 定义教师模型数量 num_teachers 为 250个，定义数据大小为240个，这是因为训练集（隐私数据）中共有60000个样本，平均分成250份给到教师模型训练，所以每一份有240个样本。

4. 按照每份240个样本的量对隐私数据进行拆分。

5. 设置模型对应的设备。

6. 定义分类器模型，后面教师模型将全部由该分类器初始化生成。

classClassifier(nn.Module):
"""
Forward Neural Network Architecture model
"""
def\_\_init\_\_(self):
super().\_\_init\_\_()
self.fc1 = nn.Linear(784,256)
self.fc2 = nn.Linear(256,128)
self.fc3 = nn.Linear(128,64)
self.fc4 = nn.Linear(64,10)
self.dropout = nn.Dropout(p=0.2)\# Dropout module with 0.2 drop probability
defforward(self,x):
x = x.view(x.shape\[0\],\-1)
x =self.dropout(F.relu(self.fc1(x)))
x =self.dropout(F.relu(self.fc2(x)))
x =self.dropout(F.relu(self.fc3(x)))
x = F.log\_softmax(self.fc4(x), dim=1)
returnx

7. 对250个教师模型进行训练，等待数分钟后，训练完成，保存所有的教师模型。

8. 将MNIST数据集中的测试集的90%用作学生模型的训练集，剩余10%用作测试集。

9. 构造学生模型的数据加载器

10. 定义教师模型的预测函数

defperdict(model,dataloader):
"""
Perdicts labels for a dataset
Input: model and dataloader
"""
outputs = torch.zeros(0, dtype=torch.long).to(device)
model.to(device)
model.eval()
forimage, labelsindataloader:
image, labels = image.to(device), labels.to(device)
output = model(image)
ps = torch.argmax(torch.exp(output), dim=1)
outputs = torch.cat((outputs, ps))
returnoutputs

11. 设置隐私等级 ε \= 0.25 ，以学生模型的训练集作为教师模型的输入来得到预测值，以此迁移教师模型的知识。对教师模型输出的预测值使用拉普拉斯分布来增加噪声，然后通过RNM算法输出得票率最高的结果，该结果作为训练数据的标签。

\# Creating the Aggregated Teacher and Student labels by combining the predictions of Teacher models
epsilon =0.25
preds = torch.zeros((len(models),9000), dtype=torch.long)
fori, modelinenumerate(models):
results = perdict(model, student\_trainloader)
preds\[i\] = results
labels = np.array(\[\]).astype(int)
forimage\_predsinnp.transpose(preds):
label\_counts = np.bincount(image\_preds, minlength =10)
beta =1/ epsilon
foriinrange(len(label\_counts)):
label\_counts\[i\] += np.random.laplace(0, beta,1)
new\_label = np.argmax(label\_counts)
labels = np.append(labels, new\_label)

12. 使用学生模型对重新标注的数据进行训练，以此来不暴露隐私的情况下获得教师模型的知识。

epochs =50
train\_losses, test\_losses = \[\], \[\]
model = Classifier()
model.to(device)
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.0001)
running\_loss =0
foreinrange(epochs):
running\_loss =0
forimages, labelsinstudent\_trainloader:
images, labels = images.to(device), labels.to(device)
optimizer.zero\_grad()
log\_ps = model(images)
loss = criterion(log\_ps, labels)
loss.backward()
optimizer.step()
running\_loss += loss.item()
else:
test\_loss =0
accuracy =0
withtorch.no\_grad():
forimages, labelsinstudent\_testloader:
images, labels = images.to(device), labels.to(device)
log\_ps = model(images)
test\_loss += criterion(log\_ps, labels)
ps = torch.exp(log\_ps)
top\_p, top\_class = ps.topk(1, dim=1)
equals = top\_class == labels.view(\*top\_class.shape)
accuracy += torch.mean(equals.type(torch.FloatTensor))
train\_losses.append(running\_loss/len(student\_trainloader))
test\_losses.append(test\_loss/len(student\_testloader))
print("Epoch: {}/{}.. ".format(e+1, epochs),
"Training Loss: {:.3f}.. ".format(running\_loss/len(student\_trainloader)),
"Test Loss: {:.3f}.. ".format(test\_loss/len(student\_testloader)),
"Test Accuracy: {:.3f}".format(accuracy/len(student\_testloader)))

13. 将训练数据的损失和测试损失通过图的形式展示出来，将得到如图2-12所示的结果。

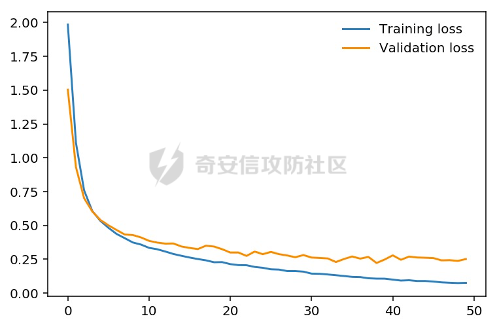
图2-12 损失对比

经过PATE模型的差分隐私保护后，测试的准确率最终达到92.8%，其准确度虽然没有直接训练时的高，但是仍然是能够接受的，毕竟这种方法能够更好的保护隐私。

0x03 参考文献

[1] Matt Fredrikson, Somesh Jha, and Thomas Ristenpart. 2015. Model Inversion Attacks that Exploit Confidence Information and Basic Countermeasures. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security (CCS '15).

[2] Papernot, Nicolas Abadi, Martín Erlingsson, Úlfar Goodfellow, Ian Talwar, Kunal. (2016). Semi-supervised Knowledge Transfer for Deep Learning from Private Training Data.

[3] https://towardsdatascience.com/understanding-differential-privacy-85ce191e198a

[4] http://www.cleverhans.io/privacy/2018/04/29/privacy-and-machine-learning.html

0x04 附件1

\# -\*- coding: utf-8 -\*-
"""dp\_example.ipynb
Automatically generated by Colaboratory.
Original file is located at
https://colab.research.google.com/drive/1eYov-YD-ds3tAJO8USpkQLukbAs93Vfd
"""
importtorch
importnumpyasnp
fromtorchvisionimportdatasets, transforms
transform = transforms.Compose(\[transforms.ToTensor(),
transforms.Normalize(\[0.5\], \[0.5\])\])#Grey Scale Image
mnist\_trainset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)#private data
mnist\_testset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)#public data
train\_loader = torch.utils.data.DataLoader(mnist\_trainset, batch\_size=64, shuffle=True)
test\_loader = torch.utils.data.DataLoader(mnist\_testset, batch\_size=64, shuffle=True)
fromtorch.utils.dataimportSubset
num\_teachers =250
teacher\_loaders = \[\]
data\_size =240\# mnist\_trainset/num\_teachers
foriinrange(num\_teachers):
indices =list(range(i\*data\_size, (i+1) \*data\_size))#creating subsets of 600 data\_size
subset\_data = Subset(mnist\_trainset, indices)
loader = torch.utils.data.DataLoader(subset\_data, batch\_size=64, num\_workers=2)
teacher\_loaders.append(loader)
device = torch.device("cuda:0"iftorch.cuda.is\_available()else"cpu")
print("Active device:", device)
fromtorchimportnn, optim
importtorch.nn.functionalasF
classClassifier(nn.Module):
"""
Forward Neural Network Architecture model
"""
def\_\_init\_\_(self):
super().\_\_init\_\_()
self.fc1 = nn.Linear(784,256)
self.fc2 = nn.Linear(256,128)
self.fc3 = nn.Linear(128,64)
self.fc4 = nn.Linear(64,10)
self.dropout = nn.Dropout(p=0.2)\# Dropout module with 0.2 drop probability
defforward(self,x):
x = x.view(x.shape\[0\],\-1)
x =self.dropout(F.relu(self.fc1(x)))
x =self.dropout(F.relu(self.fc2(x)))
x =self.dropout(F.relu(self.fc3(x)))
x = F.log\_softmax(self.fc4(x), dim=1)
returnx
epochs =10
models = \[\]
foriinrange(num\_teachers):
model = Classifier()
model.to(device)
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.0001)
running\_loss =0
teacher\_loss = \[\]
foreinrange(epochs):
running\_loss =0
forimages, labelsinteacher\_loaders\[i\]:
images, labels = images.to(device), labels.to(device)
optimizer.zero\_grad()
log\_ps = model(images)
loss = criterion(log\_ps, labels)
loss.backward()
optimizer.step()
running\_loss += loss.item()
teacher\_loss.append(running\_loss)
print("Training teacher: {}/{}.. ".format(i+1, num\_teachers),"Training Loss: {:.3f}.. ".format(running\_loss))
models.append(model)
#Creating the public dataset
student\_traindata = Subset(mnist\_testset,list(range(9000)))#90% of Test dat as train data
student\_testdata = Subset(mnist\_testset,list(range(9000,10000)))#10% of Test data as test data
student\_trainloader = torch.utils.data.DataLoader(student\_traindata, batch\_size=64, shuffle=True)
student\_testloader = torch.utils.data.DataLoader(student\_testdata, batch\_size=64, shuffle=True)
defperdict(model,dataloader):
"""
Perdicts labels for a dataset
Input: model and dataloader
"""
outputs = torch.zeros(0, dtype=torch.long).to(device)
model.to(device)
model.eval()
forimage, labelsindataloader:
image, labels = image.to(device), labels.to(device)
output = model(image)
ps = torch.argmax(torch.exp(output), dim=1)
outputs = torch.cat((outputs, ps))
returnoutputs
\# Creating the Aggregated Teacher and Student labels by combining the predictions of Teacher models
epsilon =0.25
preds = torch.zeros((len(models),9000), dtype=torch.long)
fori, modelinenumerate(models):
results = perdict(model, student\_trainloader)
preds\[i\] = results
labels = np.array(\[\]).astype(int)
forimage\_predsinnp.transpose(preds):
label\_counts = np.bincount(image\_preds, minlength =10)
beta =1/ epsilon
foriinrange(len(label\_counts)):
label\_counts\[i\] += np.random.laplace(0, beta,1)
new\_label = np.argmax(label\_counts)
labels = np.append(labels, new\_label)
student\_labels = np.array(labels)
preds = preds.numpy()
epochs =50
train\_losses, test\_losses = \[\], \[\]
model = Classifier()
model.to(device)
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.0001)
running\_loss =0
foreinrange(epochs):
running\_loss =0
forimages, labelsinstudent\_trainloader:
images, labels = images.to(device), labels.to(device)
optimizer.zero\_grad()
log\_ps = model(images)
loss = criterion(log\_ps, labels)
loss.backward()
optimizer.step()
running\_loss += loss.item()
else:
test\_loss =0
accuracy =0
withtorch.no\_grad():
forimages, labelsinstudent\_testloader:
images, labels = images.to(device), labels.to(device)
log\_ps = model(images)
test\_loss += criterion(log\_ps, labels)
ps = torch.exp(log\_ps)
top\_p, top\_class = ps.topk(1, dim=1)
equals = top\_class == labels.view(\*top\_class.shape)
accuracy += torch.mean(equals.type(torch.FloatTensor))
train\_losses.append(running\_loss/len(student\_trainloader))
test\_losses.append(test\_loss/len(student\_testloader))
print("Epoch: {}/{}.. ".format(e+1, epochs),
"Training Loss: {:.3f}.. ".format(running\_loss/len(student\_trainloader)),
"Test Loss: {:.3f}.. ".format(test\_loss/len(student\_testloader)),
"Test Accuracy: {:.3f}".format(accuracy/len(student\_testloader)))