有限域上的高次开根AMM算法在RSA上的应用

字数统计: 2.8k字   |   阅读时长≈ 13分

有限域上的高次开根AMM算法可以解决ctf部分rsa中的e和phi不互素的问题

0x01 AMM详解

对于以下式子

1.PNG

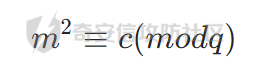
针对的是rsa中e=2的情况其实这中情况可以通过判断二次剩余的方法计算不过为了理解AMM的算法，需要另外的方式。
首先,将 q-1 写成 (2^t)*s (任何数都可以写成这一形式)对于一个二次剩余x来说，以下式子成立(欧拉定理:x可以表示为r^2)

2.PNG

把q-1的替换带进去

3.PNG

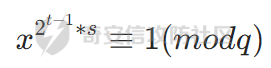
反之对于一个非二次剩余 （等于-1）

图片.png

如果此时的p-1 == 2*s ,t 的值为 1，那上述式子可写为

5.PNG

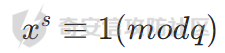
此时两边同时乘上x 再开根

6.PNG

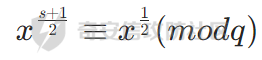
带入此时的密文（此时的加密公式为m^2 == c (mod q)）有

7.PNG

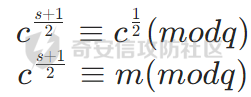
自然就解出明文了，此时的情况其实就是e为2且phi为e的倍数的情况，其实之前遇到e和phi的公因素为2的，我的办法试将m^2重新作为一个明文，使e和phi不互素，求出 m的2次方，再单独开放求解。
以上是e=2的情况，当t>=2时，也就是p = 2k*s（k>1,此时的公因数就是2）
还是回到第一个剩余式子

8.PNG

此时再开方会有以下俩种情况(这里等于1和-1涉及到证明)

9.PNG

存在开出负根的情况，我们需要让他重新变为正根，这是因为正根的后续求解比较方便，也和之前e=2的模式契合。
最好的办法就是再乘上一个同为-1的非二次剩余的项

10.PNG

然后将俩个式子合并，引入k，控制是否要乘上一个非二次剩余项

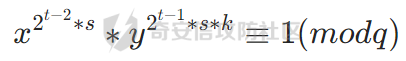
11.PNG

k=0,此时为正根，不乘，k=1,此时为负根，加上
之后不断对x开跟

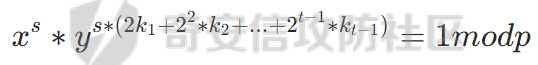
12.PNG

之后就跟之前的办法一样，先乘上一个s再开方带入c就可以了，这里的k1,k2只能在一步步计算中得出

13.PNG

就可以求解出明文了
以上问题解决的是e=2 ,m^2 = c (mod q) 的，接下来看看对于一般的e怎么处理

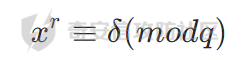
14.PNG

这里开n次方是有要求的
（1）gcd(r,q−1）= 1
（2）r | (q-1)
第一种是可以根据逆元求解，就是一般RSA的套路
主要看第二种情况
将q-1 用r表达

15.PNG

构造δ的(q-1)/r次方可以进行如下转换

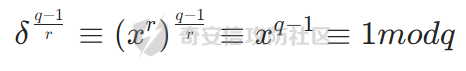
16.PNG

最后等式用到的是小费马定理
因为（r,s） = 1 ,所以可以找到一个α满足 s |(α -1)

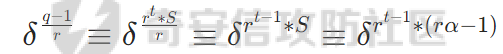
17.PNG

如果此时t=1

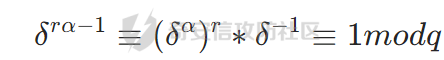
18.PNG

此时把δ再乘过去，就可以发现δα就是解了
t>=2的情况和之前处理类似，也是一直通过非剩余匹配正根
取r次非剩余ρ
非剩余满足式子如下

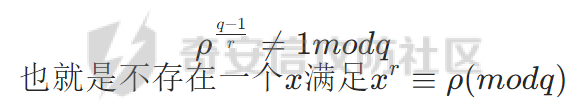
19.PNG

构造以下集合

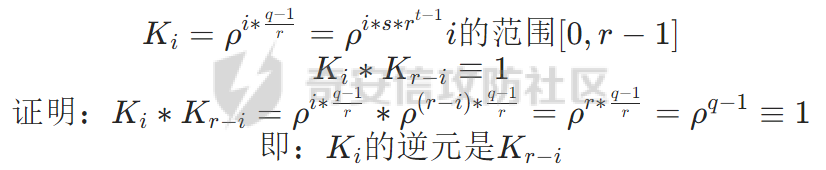
20.PNG

集合中的每隔元素的K的r都会是模1开r次方的结果，也就是每个式子都满足Ki^r=1(modq)
当i不相同时，Ki也会不相同，这是一个基于质数为群的性质
这个集合包括了每次对1 开r次方的结果
先回到这个式子

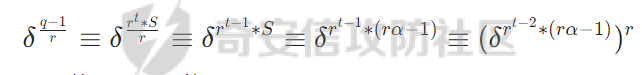
21.PNG

之后开r次方后下 (设此时等于集合中的第j个数)

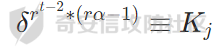
22.PNG

那这是再乘上它的逆元重新变为1

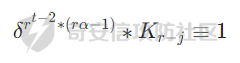
23.PNG

之后类似不断开r次方，乘上逆元，直到把消掉t,最终会得到以下式子

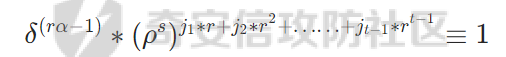
24.PNG

此时俩边先乘上δ，再提个r出来，里面包着的就是最终的解了

25.PNG

现在回到rsa上，rsa的n一般组成都是p*q
做以下转换

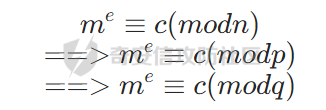
26.PNG

如果p是e的倍数就会无解吗，其实不然，这样直接开e之后，会产生e个根，上面我们可以算出一个根m0,对于剩下的e-1个根可以根据以下式子求解

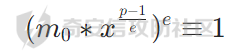
27.PNG

这样求出m1，再在m1上操作，一次得到m2,m3………………
对于上述俩个式子就会各得到e个解，俩边任意挑一个根据中国剩余定理就可以得到一个m的可能值。遍历e*e种可能性就可以了。
通过上述研究，无论是开根还是最后的求解，AMM的适用是在公因子e比较小的情况
当然如果是q不是e的倍数的话，而只是有公约数的话，可以将二者分开，先处理公因子部分，之后处理非公因子部分，根据情况具体处理。

0x02 [NCTF2019]easyRSA

一般谈到e和phi互素都会有这道题，这道题就是针对AMM进行设计的

from flag import flag
e = 0x1337
p = 199138677823743837339927520157607820029746574557746549094921488292877226509198315016018919385259781238148402833316033634968163276198999279327827901879426429664674358844084491830543271625147280950273934405879341438429171453002453838897458102128836690385604150324972907981960626767679153125735677417397078196059
q = 112213695905472142415221444515326532320352429478341683352811183503269676555434601229013679319423878238944956830244386653674413411658696751173844443394608246716053086226910581400528167848306119179879115809778793093611381764939789057524575349501163689452810148280625226541609383166347879832134495444706697124741
n = p * q
assert(flag.startswith('NCTF'))
m = int.from_bytes(flag.encode(), 'big')
assert(m.bit_length() > 1337)
c = pow(m, e, n)
print(c)
# 10562302690541901187975815594605242014385201583329309191736952454310803387032252007244962585846519762051885640856082157060593829013572592812958261432327975138581784360302599265408134332094134880789013207382277849503344042487389850373487656200657856862096900860792273206447552132458430989534820256156021128891296387414689693952047302604774923411425863612316726417214819110981605912408620996068520823370069362751149060142640529571400977787330956486849449005402750224992048562898004309319577192693315658275912449198365737965570035264841782399978307388920681068646219895287752359564029778568376881425070363592696751183359

这道题给了p,q,但p-1，q-1都是e的倍数，但e比较小，总共有0x1337^2==24196561的解，还是可以尝试破解的，
运行脚本的时间大概需要十几分钟 ，给出官方exp

import random
import time
# About 3 seconds to run
def AMM(o, r, q):
start = time.time()
print('\n----------------------------------------------------------------------------------')
print('Start to run Adleman-Manders-Miller Root Extraction Method')
print('Try to find one {:#x}th root of {} modulo {}'.format(r, o, q))
g = GF(q)
o = g(o)
p = g(random.randint(1, q))
while p ^ ((q-1) // r) == 1:
p = g(random.randint(1, q))
print('[+] Find p:{}'.format(p))
t = 0
s = q - 1
while s % r == 0:
t += 1
s = s // r
print('[+] Find s:{}, t:{}'.format(s, t))
k = 1
while (k * s + 1) % r != 0:
k += 1
alp = (k * s + 1) // r
print('[+] Find alp:{}'.format(alp))
a = p ^ (r**(t-1) * s)
b = o ^ (r*alp - 1)
c = p ^ s
h = 1
for i in range(1, t):
d = b ^ (r^(t-1-i))
if d == 1:
j = 0
else:
print('[+] Calculating DLP...')
j = - discrete_log(d, a)
print('[+] Finish DLP...')
b = b * (c^r)^j
h = h * c^j
c = c^r
result = o^alp * h
end = time.time()
print("Finished in {} seconds.".format(end - start))
print('Find one solution: {}'.format(result))
return result
def findAllPRoot(p, e):
print("Start to find all the Primitive {:#x}th root of 1 modulo {}.".format(e, p))
start = time.time()
proot = set()
while len(proot) < e:
proot.add(pow(random.randint(2, p-1), (p-1)//e, p))
end = time.time()
print("Finished in {} seconds.".format(end - start))
return proot
def findAllSolutions(mp, proot, cp, p):
print("Start to find all the {:#x}th root of {} modulo {}.".format(e, cp, p))
start = time.time()
all_mp = set()
for root in proot:
mp2 = mp * root % p
assert(pow(mp2, e, p) == cp)
all_mp.add(mp2)
end = time.time()
print("Finished in {} seconds.".format(end - start))
return all_mp
c = 10562302690541901187975815594605242014385201583329309191736952454310803387032252007244962585846519762051885640856082157060593829013572592812958261432327975138581784360302599265408134332094134880789013207382277849503344042487389850373487656200657856862096900860792273206447552132458430989534820256156021128891296387414689693952047302604774923411425863612316726417214819110981605912408620996068520823370069362751149060142640529571400977787330956486849449005402750224992048562898004309319577192693315658275912449198365737965570035264841782399978307388920681068646219895287752359564029778568376881425070363592696751183359
p = 199138677823743837339927520157607820029746574557746549094921488292877226509198315016018919385259781238148402833316033634968163276198999279327827901879426429664674358844084491830543271625147280950273934405879341438429171453002453838897458102128836690385604150324972907981960626767679153125735677417397078196059
q = 112213695905472142415221444515326532320352429478341683352811183503269676555434601229013679319423878238944956830244386653674413411658696751173844443394608246716053086226910581400528167848306119179879115809778793093611381764939789057524575349501163689452810148280625226541609383166347879832134495444706697124741
e = 0x1337
cp = c % p
cq = c % q
mp = AMM(cp, e, p)
mq = AMM(cq, e, q)
p_proot = findAllPRoot(p, e)
q_proot = findAllPRoot(q, e)
mps = findAllSolutions(mp, p_proot, cp, p)
mqs = findAllSolutions(mq, q_proot, cq, q)
print mps, mqs
def check(m):
h = m.hex()
if len(h) & 1:
return False
if h.decode('hex').startswith('NCTF'):
print(h.decode('hex'))
return True
else:
return False
# About 16 mins to run 0x1337^2 == 24196561 times CRT
start = time.time()
print('Start CRT...')
for mpp in mps:
for mqq in mqs:
solution = CRT_list([int(mpp), int(mqq)], [p, q])
if check(solution):
print(solution)
print(time.time() - start)
end = time.time()
print("Finished in {} seconds.".format(end - start))

这个脚本我是在本地搭sage环境跑的
最后可以看到有明文

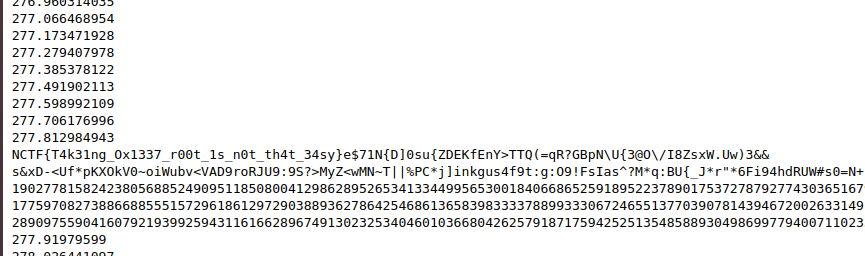
image.png

0x03 hackergame2019 十次方根

该题是上面的出题人的思路来源，可以看看,这里修改了符号，符合了rsa的规范

#!/usr/bin/env python3
p = 130095999494467643631574289251374479743427759332282644620931023932981730612064829262332840253969261363881910701276769455728130421459878658660627330362688856751252524519341435317968272275310598639991033512763704530123231772642623291899534454658707761230166809620539187116816778418242273580873637781313957589597
q = 116513882455567447431772208851676203256471727099349255694179213039239989833646726805040167642952589899809273716764673737423792812107737304956679717082391151505476360762847773608327055926832394948293052633869637754201186227370594688119795413400655007893009882742908697688490841023621108562593724732469462968731
c = 88688615046438957657148589794574470139777919686383514327296565433247300792803913489977671293854830459385807133302995575774658605472491904258624914486448276269854207404533062581134557448023142028865220726281791025833570337140263511960407206818858439353134327592503945131371190285416230131136007578355799517986306208039490339159501009668785839201465041101739825050371023956782364610889969860432267781626941824596468923354157981771773589236462813563647577651117020694251283103175874783965004467136515096081442018965974870665038880840823708377340101510978112755669470752689525778937276250835072011344062132449232775717960070624563850487919381138228636278647776184490240264110748648486121139328569423969642059474027527737521891542567351630545570488901368570734520954996585774666946913854038917494322793749823245652065062604226133920469926888309742466030087045251385865707151307850662127591419171619721200858496299127088429333831383287417361021420824398501423875648199373623572614151830871182111045650469239575676312393555191890749537174702485617397506191658938798937462708198240714491454507874141432982611857838173469612147092460359775924447976521509874765598726655964369735759375793871985156532139719500175158914354647101621378769238233
if __name__ == "__main__":
   m = int(input())
if 0 < m < z and m ** 10 % (p * q * q * q) == c:
flag = bytes.fromhex(hex(m)[2:]).decode()
if flag.startswith("flag"):
print("Flag:", flag[:32])
exit()
print("Wrong!")

先看看出题者的做法

#!/usr/bin/env python3
from sympy.ntheory.residue_ntheory import sqrt_mod
import sympy.ntheory.residue_ntheory
import gmpy2
def factor_(nn, *args, **kwargs):
t = 0
while nn % p == 0:
t += 1
nn //= p
s = 0
while nn % q == 0:
s += 1
nn //= q
if nn != 1:
print(nn)
return None
return {p: t, q: s}
sympy.ntheory.residue_ntheory.factorint = factor_
n = p * q ** 3
phi = (p - 1) * (q ** 2) * (q - 1)
root_5th_of_c = pow(c, gmpy2.invert(5, phi // 5), n)
root_5th_of_1_all = set(pow(i, (phi // 5), n) for i in range(1, 20))
root_5th_of_1_all = set(r for r in set(root_5th_of_1_all) if pow(r, 5, n) == 1)
root_5th_of_c_all = [root_5th_of_c * r % n for r in root_5th_of_1_all]
m_all = [m for r in root_5th_of_c_all for m in sqrt_mod(r, n, True)]
'''
sqrt_mod用法
print(sqrt_mod(1, 3, True))
[1, 2]
'''
print(len(m_all))
for m in m_all:
h = hex(m)[2:]
if len(h) % 2 == 0 and bytes.fromhex(hex(m)[2:]).startswith(b"flag"):
print(bytes.fromhex(hex(m)[2:]).decode()[:32])

总体思路就是先对c开一次5次方，因为不互素，这样的解不止一个，之后久枚举了对1开5次方的根（1-20），和第一次得到的c的5次方方根相乘得到所有的c的5次方根，之后枚举所有能够平方的，枚举明文。

之后如果使用AMM算法，在crt时遇到一个问题，就是m的实际大小是大于pq的，主要是m后面添加了很多随机字符,这就很尴尬了，为了使AMM算法起示例作用，这里更改一下m的大小，小于p*q ,

现题目如下

p = 130095999494467643631574289251374479743427759332282644620931023932981730612064829262332840253969261363881910701276769455728130421459878658660627330362688856751252524519341435317968272275310598639991033512763704530123231772642623291899534454658707761230166809620539187116816778418242273580873637781313957589597
q = 116513882455567447431772208851676203256471727099349255694179213039239989833646726805040167642952589899809273716764673737423792812107737304956679717082391151505476360762847773608327055926832394948293052633869637754201186227370594688119795413400655007893009882742908697688490841023621108562593724732469462968731
c = 126808777970890909395969111513826891776178832617042814774375552600695688153718861654784351886071810119874140980456611394580200350101088845290666301837289315327270952139607630997965276620380921725477409882463011982731424681180047831979110335471391930182567380277703580309793741012685095447538187714360457182040336841071380124549207751913139060425320305495200059850500837424195024446528340859137378082448350646834868010608194218154894845945825583856429272543748472462300307083605387827178223188342571722648567896758307433722544362785881815585954706959450156217485796489653685347256661387003349070988543010381034882551300838190577280153778825095768256953986605895380647312148295996322796282362919641048955292163986490400994601213844393520313549457397531453954489470528902939956743562977625790182780825889097932364691809964679802077108043319121681473531999745782934904703903400198431097094872604137491802391995915694538693011322181188382253801249633900234020656568735952960628328978038586226354610531227424504541866785514535787306610222582291292672734216136365360711231891247539712205459663339920031344645851719630203705933738516926451124498511640658152936417123433600747361352218661471387119036053850354611449789875280268879261972595328
if __name__ == "__main__":
   m = int(input())
if 0 < m < c and m ** 10 % (p * q * q * q) == c:
flag = bytes.fromhex(hex(m)[2:]).decode()
if flag.startswith("flag"):
print("Flag:", flag[:32])
exit()
print("Wrong!")

方法有点小改动，分为俩部分，一个求m%p,一个求m%q

m%p

import gmpy2
from sympy.ntheory.residue_ntheory import sqrt_mod
e = 10
p = 130095999494467643631574289251374479743427759332282644620931023932981730612064829262332840253969261363881910701276769455728130421459878658660627330362688856751252524519341435317968272275310598639991033512763704530123231772642623291899534454658707761230166809620539187116816778418242273580873637781313957589597
q = 116513882455567447431772208851676203256471727099349255694179213039239989833646726805040167642952589899809273716764673737423792812107737304956679717082391151505476360762847773608327055926832394948293052633869637754201186227370594688119795413400655007893009882742908697688490841023621108562593724732469462968731
c = 126808777970890909395969111513826891776178832617042814774375552600695688153718861654784351886071810119874140980456611394580200350101088845290666301837289315327270952139607630997965276620380921725477409882463011982731424681180047831979110335471391930182567380277703580309793741012685095447538187714360457182040336841071380124549207751913139060425320305495200059850500837424195024446528340859137378082448350646834868010608194218154894845945825583856429272543748472462300307083605387827178223188342571722648567896758307433722544362785881815585954706959450156217485796489653685347256661387003349070988543010381034882551300838190577280153778825095768256953986605895380647312148295996322796282362919641048955292163986490400994601213844393520313549457397531453954489470528902939956743562977625790182780825889097932364691809964679802077108043319121681473531999745782934904703903400198431097094872604137491802391995915694538693011322181188382253801249633900234020656568735952960628328978038586226354610531227424504541866785514535787306610222582291292672734216136365360711231891247539712205459663339920031344645851719630203705933738516926451124498511640658152936417123433600747361352218661471387119036053850354611449789875280268879261972595328
n = p * q ** 3
phi = (p - 1) * (q ** 2) * (q - 1)
c1 = c%p
d = gmpy2.invert(5,p-1)
c1 = pow(c1,d,p)
print(sqrt_mod(c1,p,True))
#求出m%p的俩个解

p-1只是2的倍数，所以可以求逆元得到m2的值，再继续开方，可以得到俩个解

import random
import time
from Crypto.Util.number import *
# About 3 seconds to run
def AMM(o, r, q):
g = GF(q)
o = g(o)
p = g(random.randint(1, q))
while p ^ ((q-1) // r) == 1:
p = g(random.randint(1, q))
t = 0
s = q - 1
while s % r == 0:
t += 1
s = s // r
k = 1
while (k * s + 1) % r != 0:
k += 1
alp = (k * s + 1) // r
a = p ^ (r**(t-1) * s)
b = o ^ (r*alp - 1)
c = p ^ s
h = 1
for i in range(1, t):
d = b ^ (r^(t-1-i))
if d == 1:
j = 0
else:
j = - discrete_log(d, a)
b = b * (c^r)^j
h = h * c^j
c = c^r
result = o^alp * h
return result
def findAllPRoot(p, e):
proot = set()
while len(proot) < e:
proot.add(pow(random.randint(2, p-1), (p-1)//e, p))
return proot
def findAllSolutions(mp, proot, cp, p):
all_mp = set()
for root in proot:
mp2 = mp * root % p
assert(pow(mp2, e, p) == cp)
all_mp.add(mp2)
return all_mp
e = 10
p = 130095999494467643631574289251374479743427759332282644620931023932981730612064829262332840253969261363881910701276769455728130421459878658660627330362688856751252524519341435317968272275310598639991033512763704530123231772642623291899534454658707761230166809620539187116816778418242273580873637781313957589597
q = 116513882455567447431772208851676203256471727099349255694179213039239989833646726805040167642952589899809273716764673737423792812107737304956679717082391151505476360762847773608327055926832394948293052633869637754201186227370594688119795413400655007893009882742908697688490841023621108562593724732469462968731
c = 126808777970890909395969111513826891776178832617042814774375552600695688153718861654784351886071810119874140980456611394580200350101088845290666301837289315327270952139607630997965276620380921725477409882463011982731424681180047831979110335471391930182567380277703580309793741012685095447538187714360457182040336841071380124549207751913139060425320305495200059850500837424195024446528340859137378082448350646834868010608194218154894845945825583856429272543748472462300307083605387827178223188342571722648567896758307433722544362785881815585954706959450156217485796489653685347256661387003349070988543010381034882551300838190577280153778825095768256953986605895380647312148295996322796282362919641048955292163986490400994601213844393520313549457397531453954489470528902939956743562977625790182780825889097932364691809964679802077108043319121681473531999745782934904703903400198431097094872604137491802391995915694538693011322181188382253801249633900234020656568735952960628328978038586226354610531227424504541866785514535787306610222582291292672734216136365360711231891247539712205459663339920031344645851719630203705933738516926451124498511640658152936417123433600747361352218661471387119036053850354611449789875280268879261972595328
cq = c % q
mq = AMM(cq, e, q)
q_proot = findAllPRoot(q, e)
#m%q的10个解
mqs = findAllSolutions(mq, q_proot, cq, q)
mps = [3008148103208720665270181485208403652450928909814855464752252181939928951812772634333412340830242763280573185160437132927955272197800486077706200362165829887266204983589842953772797775415945762217985338391754707489063277439031014673438578332622828149358172463561103137649245303378078471322173851503335479030, 127087851391258922966304107766166076090976830422467789156178771751041801660252056627999427913139018600601337516116332322800175149262078172582921130000523026863986319535751592364195474499894652877773048174371949822634168495203592277226095876326084933080808637156978083979167533114864195109551463929810622110567]
def check(m):
h = m.hex()
if len(h) & 1:
return False
if h.decode('hex').startswith('NCTF'):
print(h.decode('hex'))
return True
else:
return False
for mpp in mps:
for mqq in mqs:
solution = CRT_list([int(mpp), int(mqq)], [p, q])
if(long_to_bytes(solution).startswith(b'flag')):
print(long_to_bytes(solution))

这里求出m%q总共有10个解，再和之前的m%p的2个解分别进行中国剩余定理，就可以得到预定的m

image-20220609113107-z658wy0.png

e=10在这里并不能很好展开AMM算法的优越性，不过只要e位于一个较大（e*e有上限）的情况，AMM算法是可以较好解决这类问题的
有兴趣的可以看看原版paper https://arxiv.org/pdf/1111.4877.pdf
easyrsa_wp：https://blog.soreatu.com/posts/intended-solution-to-crypto-problems-in-nctf-2019/#easyrsa909pt-2solvers


赏

谢谢你请我吃糖果

支付宝
微信

扫一扫，分享到微信

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia-plus根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

俗话说“好记性不如烂笔头”，各个安全社区各自为战，当我们想要搜索某一方面的文章的时候总是得在各个平台之间来回横跳，于是乎，一个平台文章聚合搜索的想法诞生了。
然后正好我想有一个自己的博客，于是乎两者融合在了一起。
下面简单介绍各个导航的区别：
个人文章：本人的笔记、复现、总结等或者本人参与的共同创作。
收集文章：手工从公众号收集保存的文章，更新频率看本人喜好所以比较慢。
聚合文章：从各大平台收集整理，由工具实现，每天更新。
很惭愧，只做了一点微小的工作。