ECC浅析和在ctf中的应用

英文全称：Ellipse Curve Cryptography，也即椭圆曲线密码 首先是要了解为什么要使用ECC加密 主要原因是ECC的较短的密钥就可以达到相同级别RSA长的多的密钥安全，一般认为ECC的160bit密钥的强度和1024bit的RSA密钥强度相当，使用短的密钥的好处在于加解密速度快、节省能源、节省带宽、存储空间。比特币以及中国的二代身份证都使用了256 比特的椭圆曲线密码算法。所以了解ECC的是非常有必要的。 这里还是从加解密的步骤进行，之后再加入解题的部分 首先我们必须了解这些加密的的安全性是从哪来的，就拿RSA举例，破解RSA的根本就是解决一个大数分解问题，一般解RSA相关的题目也就是以拿到n的因子为目标导向。 对于ECC而言，基于的式子如下

  Q = k P*

这里的Q,P都是在椭圆曲线的俩个点，

k是一个整数 如果你知道k和P的，求解Q是很容易的

但如果你知道Q,P，求解k是很困难的，该问题也叫椭圆曲线离散对数问题

所以一般我们将k作为密钥使用，这里的k非常大，保证不能被穷举

这里面涉及到的运算在之后会讲解

椭圆曲线

这里的椭圆曲线基本上和高中涉及到的椭圆方程没有联系，命名原因是因为其表达的式子的形式和椭圆的周长式子比较类似。椭圆曲线就是三次平滑代数平面曲线

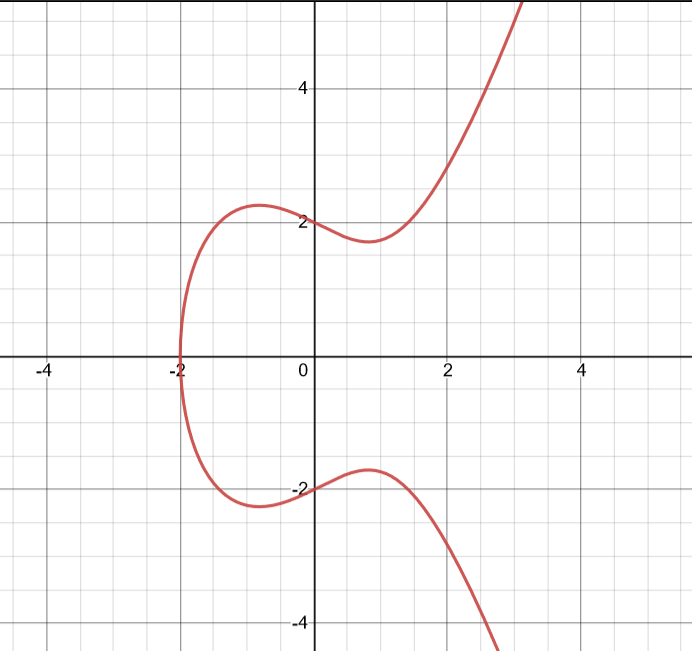
一个例子函数表达式为y^2 = x^3 + ax + b，上面的函数形式为y^2 = x^3 -2x +4 同时这里a,b要满足4*a^3 +27b^2 != 0的要求，这样是确保不会出现奇点，也就是不可导的点 #### 加法运算

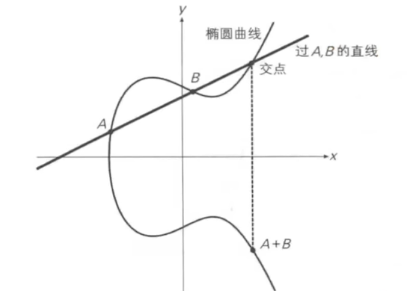
这里计算的是A+B的计算流程，得出的结果也是一个点

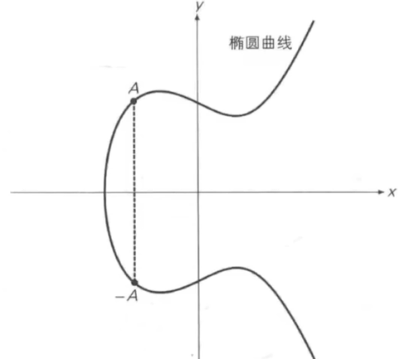
如果A+(-A)这种情况，它定义了一个无穷远点，类似的都等于这个，不过在加密中这种情况不会出现。

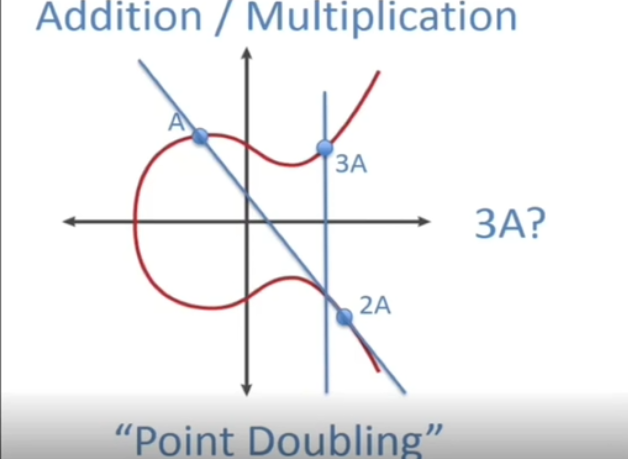
3A = A + 2A 接下来来看看ECC为什么能保证无法用Q，P求出k来，这里的P是基点，可以看到每加一个P,都会有很大的改变，而且其变化是很没有规律的，具体数学的证明涉及可证明安全部分。

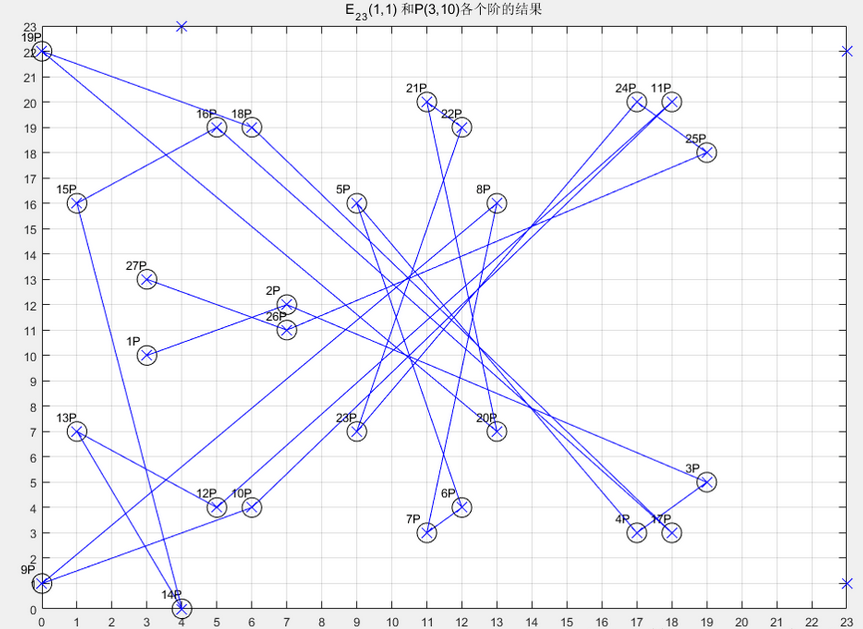
加密及解密

1.选择一条椭圆曲线Ep(a,b)，并且选取曲线上的一点作为基点 P

2.选定一个大数k作为私钥，并计算生成公钥Q=kP

3.加密：选择一个随机数r，将消息M生成密文C 密文也是一个点对，即加密的数据为（rP,M+rQ）

4.解密： 使用密文点对：y-kx = M M + rQ - k(rP) == M +rkP - krp = M 以上就是大概的ECC的操作，之后是一些相关数学知识的简介

有限域

虽然看的有点高大上，其实原理很简单 椭圆曲线是连续的，这对加密来说是不合适的，所以我们要将椭圆曲线变成一个一个离散的点 这就要把椭圆曲线定义在有限域上。

域简单来说就是一个集合，不过针对这个集合，你可以任意选择俩个元素进行加减乘除之后得到的结果依然属于这个集合，这些数就可以组合成一个域。 有理数集合，实数集合，复数集合都是域，但整数集合因为使用除法会产生小数，所以不是一个域。 无限域就是集合元素个数无限，有限域元素有限 有限域中的元素的个数成为有限域的阶 每个有限域的阶一定为质数的幂，即有限域的阶可以表示为p^n(p为素数，n是正整数)，该有限域可记为GF(p^n)

有限域上的椭圆曲线

直接对计算结果mod p，就可将将椭圆曲线转换成一个域（p为素数），当然它满足交换率，结合率，分配律等。取模产生的域天然是一个群，这里关于群的知识不进行扩充，主要还是针对椭圆曲线的加密。

椭圆曲线的计算

先贴一张图，这里计算A(x1,y1) + B (x2,y2) = C (x3,y3)的过程 以及A+A = 2A的过程

例题：

方程为y2≡x3+x+1 mod 23 。曲线全部点如下

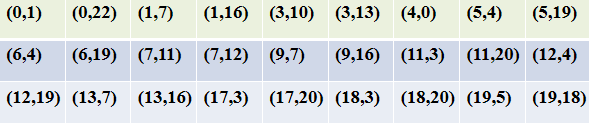
1）

已知P=(3,10)，Q=(9,7)，求P+Q

2）

求2P 1）求P+Q

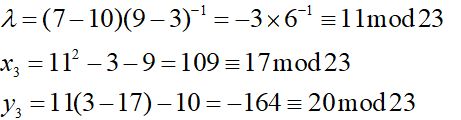
所以P+Q=（17,20） 2）求2P

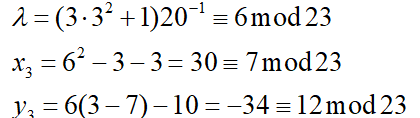
所以2P=(7,12) 其加密流程大概如上，但还有一个问题就是k一般是非常大，一个一个计算效率绝对很低 这里一般的处理思路和快速幂类似

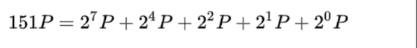
这样只要计算2P,4P,8P………………就可以了

ctf例题

[watevrCTF 2019]ECC-RSA

from fastecdsa.curve import P521 as Curve
from fastecdsa.point import Point
from Crypto.Util.number import bytes_to_long, isPrime
from os import urandom
from random import getrandbits
def gen_rsa_primes(G):
urand = bytes_to_long(urandom(521//8))
while True:
s = getrandbits(521) ^ urand
Q = s*G
if isPrime(Q.x) and isPrime(Q.y):
print("ECC Private key:", hex(s))
print("RSA primes:", hex(Q.x), hex(Q.y))
print("Modulo:", hex(Q.x * Q.y))
return (Q.x, Q.y)
flag = int.from_bytes(input(), byteorder="big")
ecc_p = Curve.p
a = Curve.a
b = Curve.b
Gx = Curve.gx
Gy = Curve.gy
G = Point(Gx, Gy, curve=Curve)
e = 0x10001
p, q = gen_rsa_primes(G)
n = p*q
file_out = open("downloads/ecc-rsa.txt", "w")
file_out.write("ECC Curve Prime: " + hex(ecc_p) + "\n")
file_out.write("Curve a: " + hex(a) + "\n")
file_out.write("Curve b: " + hex(b) + "\n")
file_out.write("Gx: " + hex(Gx) + "\n")
file_out.write("Gy: " + hex(Gy) + "\n")
file_out.write("e: " + hex(e) + "\n")
file_out.write("p * q: " + hex(n) + "\n")
c = pow(flag, e, n)
file_out.write("ciphertext: " + hex(c) + "\n")

加了个rsa，但关键问题还是破解ECC, 现在的p,q就是 Q=kP之后的点对 输出的文件如下

ECC Curve Prime: 0x1ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
Curve a: -0x3
Curve b: 0x51953eb9618e1c9a1f929a21a0b68540eea2da725b99b315f3b8b489918ef109e156193951ec7e937b1652c0bd3bb1bf073573df883d2c34f1ef451fd46b503f00
Gx: 0xc6858e06b70404e9cd9e3ecb662395b4429c648139053fb521f828af606b4d3dbaa14b5e77efe75928fe1dc127a2ffa8de3348b3c1856a429bf97e7e31c2e5bd66
Gy: 0x11839296a789a3bc0045c8a5fb42c7d1bd998f54449579b446817afbd17273e662c97ee72995ef42640c550b9013fad0761353c7086a272c24088be94769fd16650
e: 0x10001
p * q: 0x118aaa1add80bdd0a1788b375e6b04426c50bb3f9cae0b173b382e3723fc858ce7932fb499cd92f5f675d4a2b05d2c575fc685f6cf08a490d6c6a8a6741e8be4572adfcba233da791ccc0aee033677b72788d57004a776909f6d699a0164af514728431b5aed704b289719f09d591f5c1f9d2ed36a58448a9d57567bd232702e9b28f
ciphertext: 0x3862c872480bdd067c0c68cfee4527a063166620c97cca4c99baff6eb0cf5d42421b8f8d8300df5f8c7663adb5d21b47c8cb4ca5aab892006d7d44a1c5b5f5242d88c6e325064adf9b969c7dfc52a034495fe67b5424e1678ca4332d59225855b7a9cb42db2b1db95a90ab6834395397e305078c5baff78c4b7252d7966365afed9e

已知a,b，那这个椭圆曲线就已知了

   $*y2 = x3 + ax + b*$

我们又知道了p，q是满足上述的式子，可以带入，又已知p*q = n ,

$q^2 = p^3 + ap +b$ 
$p*q = n$ 

将式子带入乘法里

  $q = \sqrt{p^3 + ap +b}$
 $\sqrt{p^3 + ap +b} *p = n$
  $p^5 + ap^3 +bx^2 = n^2$

最后化为一个一元五次方的方程，这个p因为很大，一般是求解不出来的，但这个式子在有限域中也成立，就是mod **P(大写)**成立，那我们就放在sage上跑一下

a = -0x3
b = 0x51953eb9618e1c9a1f929a21a0b68540eea2da725b99b315f3b8b489918ef109e156193951ec7e937b1652c0bd3bb1bf073573df883d2c34f1ef451fd46b503f00
n = 0x118aaa1add80bdd0a1788b375e6b04426c50bb3f9cae0b173b382e3723fc858ce7932fb499cd92f5f675d4a2b05d2c575fc685f6cf08a490d6c6a8a6741e8be4572adfcba233da791ccc0aee033677b72788d57004a776909f6d699a0164af514728431b5aed704b289719f09d591f5c1f9d2ed36a58448a9d57567bd232702e9b28f
p = 0x1ffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
PR.<x> = PolynomialRing(Zmod(p))
f=x^5+a*x^3 + b*x^2 - n^2
roots=f.roots()
print(roots)

最后得到三个解，第二个解符合要求，此时得到了p，q,按照rsa的模板求解即可

import gmpy2
from Crypto.Util.number import *
n = 0x118aaa1add80bdd0a1788b375e6b04426c50bb3f9cae0b173b382e3723fc858ce7932fb499cd92f5f675d4a2b05d2c575fc685f6cf08a490d6c6a8a6741e8be4572adfcba233da791ccc0aee033677b72788d57004a776909f6d699a0164af514728431b5aed704b289719f09d591f5c1f9d2ed36a58448a9d57567bd232702e9b28f
p = 4573744216059593260686660411936793507327994800883645562370166075007970317346237399760397301505506131100113886281839847419425482918932436139080837246914736557
q = n//p
e = 65537
c = 0x3862c872480bdd067c0c68cfee4527a063166620c97cca4c99baff6eb0cf5d42421b8f8d8300df5f8c7663adb5d21b47c8cb4ca5aab892006d7d44a1c5b5f5242d88c6e325064adf9b969c7dfc52a034495fe67b5424e1678ca4332d59225855b7a9cb42db2b1db95a90ab6834395397e305078c5baff78c4b7252d7966365afed9e
d = gmpy2.invert(e,(p-1)*(q-1))
print(long_to_bytes(pow(c,d,n)))

椭圆曲线画图

sage