2022 ACTF impossible RSA

from Crypto.Util.number import *
from Crypto.PublicKey import RSA
e = 65537
flag = b'ACTF{...}'
while True:
p = getPrime(1024)
q = inverse(e, p)
if not isPrime(q):
continue
n = p * q;
public = RSA.construct((n, e))
with open("public.pem", "wb") as file:
file.write(public.exportKey('PEM'))
with open("flag", "wb") as file:
file.write(long_to_bytes(pow(bytes_to_long(flag), e, n)))
break

这里条件的就是

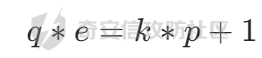
俩边再同时乘上p就有

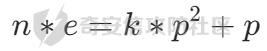
此时可以测一下k的大小,发现是比较小的,自己生成几个样例可以发现

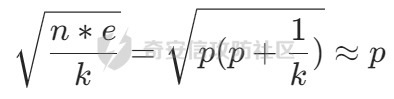
那就遍历一遍k，找出合适的p求解即可

c = bytes_to_long(open("flag","rb").read())
n = 15987576139341888788648863000534417640300610310400667285095951525208145689364599119023071414036901060746667790322978452082156680245315967027826237720608915093109552001033660867808508307569531484090109429319369422352192782126107818889717133951923616077943884651989622345435505428708807799081267551724239052569147921746342232280621533501263115148844736900422712305937266228809533549134349607212400851092005281865296850991469375578815615235030857047620950536534729591359236290249610371406300791107442098796128895918697534590865459421439398361818591924211607651747970679849262467894774012617335352887745475509155575074809
e = 65537
for k in range(2,10000000):
q = gmpy2.iroot(n*e//k,2)[0]
p = n//q
if p == 1:
continue
if p*q == n:
d = gmpy2.invert(e,(p-1)*(q-1))
print(long_to_bytes(pow(c,d,n)))
b'ACTF{F1nD1nG_5pEcia1_n_i5_nOt_eA5y}'

2022 ACTF RSA LEAK

from sage.all import *
from secret import flag
from Crypto.Util.number import bytes_to_long
def leak(a, b):
p = random_prime(pow(2, 64))
q = random_prime(pow(2, 64))
n = p*q
e = 65537
print(n)
print((pow(a, e) + pow(b, e) + 0xdeadbeef) % n)
def gen_key():
a = randrange(0, pow(2,256))
b = randrange(0, pow(2,256))
p = pow(a, 4)
q = pow(b, 4)
rp = randrange(0, pow(2,24))
rq = randrange(0, pow(2,24))
pp = next_prime(p+rp)
qq = next_prime(q+rq)
if pp % pow(2, 4) == (pp-p) % pow(2, 4) and qq % pow(2, 4) == (qq-q) % pow(2, 4):
n = pp*qq
rp = pp-p
rq = qq-q
return n, rp, rq
n, rp, rq = gen_key()
e = 65537
c = pow(bytes_to_long(flag), e, n)
print("n =", n)
print("e =", e)
print("c =", c)
print("=======leak=======")
leak(rp, rq)
'''
n = 3183573836769699313763043722513486503160533089470716348487649113450828830224151824106050562868640291712433283679799855890306945562430572137128269318944453041825476154913676849658599642113896525291798525533722805116041675462675732995881671359593602584751304602244415149859346875340361740775463623467503186824385780851920136368593725535779854726168687179051303851797111239451264183276544616736820298054063232641359775128753071340474714720534858295660426278356630743758247422916519687362426114443660989774519751234591819547129288719863041972824405872212208118093577184659446552017086531002340663509215501866212294702743
e = 65537
c = 48433948078708266558408900822131846839473472350405274958254566291017137879542806238459456400958349315245447486509633749276746053786868315163583443030289607980449076267295483248068122553237802668045588106193692102901936355277693449867608379899254200590252441986645643511838233803828204450622023993363140246583650322952060860867801081687288233255776380790653361695125971596448862744165007007840033270102756536056501059098523990991260352123691349393725158028931174218091973919457078350257978338294099849690514328273829474324145569140386584429042884336459789499705672633475010234403132893629856284982320249119974872840
=======leak=======
122146249659110799196678177080657779971
90846368443479079691227824315092288065

先看leak部分
输入的rp,rq都只有24位，这里就可以进行爆破，爆破的条件是长度要小于24位
得到正确的rq，rp

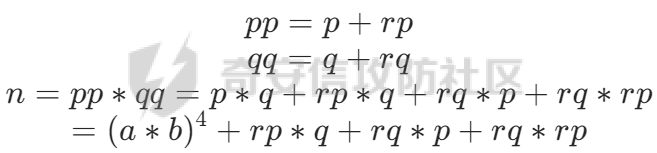
因为a和b都很大，直接开四次方是可以直接算出的
算出a*b
这样带回原式乘上p（或q）就是一个一元二次方程求解，解出来即可

import gmpy2
from Crypto.Util.number import *
n1 = 122146249659110799196678177080657779971
p1 = 8949458376079230661
q1 = 13648451618657980711
e1 = 65537
d1 = gmpy2.invert(e1,(p1-1)*(q1-1))
c1 = 90846368443479079691227824315092288065
n = 3183573836769699313763043722513486503160533089470716348487649113450828830224151824106050562868640291712433283679799855890306945562430572137128269318944453041825476154913676849658599642113896525291798525533722805116041675462675732995881671359593602584751304602244415149859346875340361740775463623467503186824385780851920136368593725535779854726168687179051303851797111239451264183276544616736820298054063232641359775128753071340474714720534858295660426278356630743758247422916519687362426114443660989774519751234591819547129288719863041972824405872212208118093577184659446552017086531002340663509215501866212294702743
e = 65537
c = 48433948078708266558408900822131846839473472350405274958254566291017137879542806238459456400958349315245447486509633749276746053786868315163583443030289607980449076267295483248068122553237802668045588106193692102901936355277693449867608379899254200590252441986645643511838233803828204450622023993363140246583650322952060860867801081687288233255776380790653361695125971596448862744165007007840033270102756536056501059098523990991260352123691349393725158028931174218091973919457078350257978338294099849690514328273829474324145569140386584429042884336459789499705672633475010234403132893629856284982320249119974872840
'''
for i in range(2**24):
c11 = (c1 - 0xdeadbeef - pow(i,e1,n1))%n1
rp = pow(c11,d1,n1)
if len(bin(rp))<=26:
rq = i
print(rp)
print(i)
break
'''
rp = 11974933
rq = 405771
a_mul_b = (gmpy2.iroot(n,4)[0])**4
s = n - rp*rq - a_mul_b
#  rq*p^2  - s*p + rp*a_mul_b
delta = s**2 - 4*rq*rp*a_mul_b
p = (s-gmpy2.iroot(delta,2)[0])//(2*rq)
pp = p+rp
qq = n//pp
print(pp*qq == n)
d = gmpy2.invert(65537,(pp-1)*(qq-1))
print(long_to_bytes(pow(c,d,n)))
#b'ACTF{lsb_attack_in_RSA|a32d7f}'

GKCTF 2021 RRRRsa

from Crypto.Util.number import *
from gmpy2 import gcd
flag = b'xxxxxxxxxxxxx'
p = getPrime(512)
q = getPrime(512)
m = bytes_to_long(flag)
n = p*q
e = 65537
c = pow(m,e,n)
print('c={}'.format(c))
p1 = getPrime(512)
q1 = getPrime(512)
n1 = p1*q1
e1 = 65537
assert gcd(e1,(p1-1)*(q1-1)) == 1
c1 = pow(p,e1,n1)
print('n1={}'.format(n1))
print('c1={}'.format(c1))
hint1 = pow(2020 * p1 + q1, 202020, n1)
hint2 = pow(2021 * p1 + 212121, q1, n1)
print('hint1={}'.format(hint1))
print('hint2={}'.format(hint2))
p2 = getPrime(512)
q2 = getPrime(512)
n2 = p2*q2
e2 = 65537
assert gcd(e1,(p2-1)*(q2-1)) == 1
c2 = pow(q,e2,n2)
hint3 = pow(2020 * p2 + 2021 * q2, 202020, n2)
hint4 = pow(2021 * p2 + 2020 * q2, 212121, n2)
print('n2={}'.format(n2))
print('c2={}'.format(c2))
print('hint3={}'.format(hint3))
print('hint4={}'.format(hint4))
#c=13492392717469817866883431475453770951837476241371989714683737558395769731416522300851917887957945766132864151382877462142018129852703437240533684604508379950293643294877725773675505912622208813435625177696614781601216465807569201380151669942605208425645258372134465547452376467465833013387018542999562042758
#n1=75003557379080252219517825998990183226659117019770735080523409561757225883651040882547519748107588719498261922816865626714101556207649929655822889945870341168644508079317582220034374613066751916750036253423990673764234066999306874078424803774652754587494762629397701664706287999727238636073466137405374927829
#c1=68111901092027813007099627893896838517426971082877204047110404787823279211508183783468891474661365139933325981191524511345219830693064573462115529345012970089065201176142417462299650761299758078141504126185921304526414911455395289228444974516503526507906721378965227166653195076209418852399008741560796631569
#hint1=23552090716381769484990784116875558895715552896983313406764042416318710076256166472426553520240265023978449945974218435787929202289208329156594838420190890104226497263852461928474756025539394996288951828172126419569993301524866753797584032740426259804002564701319538183190684075289055345581960776903740881951
#hint2=52723229698530767897979433914470831153268827008372307239630387100752226850798023362444499211944996778363894528759290565718266340188582253307004810850030833752132728256929572703630431232622151200855160886614350000115704689605102500273815157636476901150408355565958834764444192860513855376978491299658773170270
#n2=114535923043375970380117920548097404729043079895540320742847840364455024050473125998926311644172960176471193602850427607899191810616953021324742137492746159921284982146320175356395325890407704697018412456350862990849606200323084717352630282539156670636025924425865741196506478163922312894384285889848355244489
#c2=67054203666901691181215262587447180910225473339143260100831118313521471029889304176235434129632237116993910316978096018724911531011857469325115308802162172965564951703583450817489247675458024801774590728726471567407812572210421642171456850352167810755440990035255967091145950569246426544351461548548423025004
#hint3=25590923416756813543880554963887576960707333607377889401033718419301278802157204881039116350321872162118977797069089653428121479486603744700519830597186045931412652681572060953439655868476311798368015878628002547540835719870081007505735499581449077950263721606955524302365518362434928190394924399683131242077
#hint4=104100726926923869566862741238876132366916970864374562947844669556403268955625670105641264367038885706425427864941392601593437305258297198111819227915453081797889565662276003122901139755153002219126366611021736066016741562232998047253335141676203376521742965365133597943669838076210444485458296240951668402513

根据提示分别求出p,q,最后再得到明文

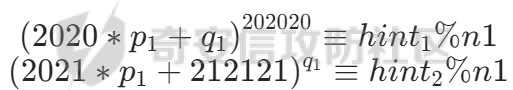
首先要将他们拆开来处理

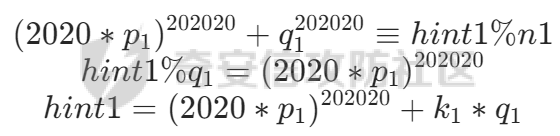
针对hint2使用费马小定理 a^（p-1）≡1（mod p）

最终得到了hint1和hint2的表达式，但俩者的表达是不一样的，这里还需要做一些转换，将二者形式统一

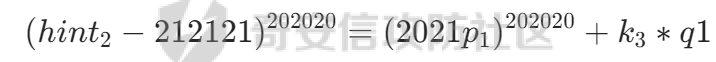
现在到这就比较明朗了，需要将二者前面一堆减去，之后剩下的就可以通过gcd求出公共因子q1
这里处理的话是将hint1乘上2021^202020,hint2部分乘上2020^202020.这样它前面部分是相等的
对应的hint3和hint4类似可以将q2求出来，之后将p,q解出来之后得到flag

from gmpy2 import gcd
from Crypto.Util.number import *
import gmpy2
c=13492392717469817866883431475453770951837476241371989714683737558395769731416522300851917887957945766132864151382877462142018129852703437240533684604508379950293643294877725773675505912622208813435625177696614781601216465807569201380151669942605208425645258372134465547452376467465833013387018542999562042758
n1=75003557379080252219517825998990183226659117019770735080523409561757225883651040882547519748107588719498261922816865626714101556207649929655822889945870341168644508079317582220034374613066751916750036253423990673764234066999306874078424803774652754587494762629397701664706287999727238636073466137405374927829
c1=68111901092027813007099627893896838517426971082877204047110404787823279211508183783468891474661365139933325981191524511345219830693064573462115529345012970089065201176142417462299650761299758078141504126185921304526414911455395289228444974516503526507906721378965227166653195076209418852399008741560796631569
hint1=23552090716381769484990784116875558895715552896983313406764042416318710076256166472426553520240265023978449945974218435787929202289208329156594838420190890104226497263852461928474756025539394996288951828172126419569993301524866753797584032740426259804002564701319538183190684075289055345581960776903740881951
hint2=52723229698530767897979433914470831153268827008372307239630387100752226850798023362444499211944996778363894528759290565718266340188582253307004810850030833752132728256929572703630431232622151200855160886614350000115704689605102500273815157636476901150408355565958834764444192860513855376978491299658773170270
n2=114535923043375970380117920548097404729043079895540320742847840364455024050473125998926311644172960176471193602850427607899191810616953021324742137492746159921284982146320175356395325890407704697018412456350862990849606200323084717352630282539156670636025924425865741196506478163922312894384285889848355244489
c2=67054203666901691181215262587447180910225473339143260100831118313521471029889304176235434129632237116993910316978096018724911531011857469325115308802162172965564951703583450817489247675458024801774590728726471567407812572210421642171456850352167810755440990035255967091145950569246426544351461548548423025004
hint3=25590923416756813543880554963887576960707333607377889401033718419301278802157204881039116350321872162118977797069089653428121479486603744700519830597186045931412652681572060953439655868476311798368015878628002547540835719870081007505735499581449077950263721606955524302365518362434928190394924399683131242077
hint4=104100726926923869566862741238876132366916970864374562947844669556403268955625670105641264367038885706425427864941392601593437305258297198111819227915453081797889565662276003122901139755153002219126366611021736066016741562232998047253335141676203376521742965365133597943669838076210444485458296240951668402513
e=65537
q1 = gcd(n1,pow(hint2-212121,202020,n1)*pow(2020,202020,n1)-hint1*pow(2021,202020,n1))
p1 = n1//q1
q2 = gcd(n2,pow(hint3,212121,n2)*pow(2021,202020*212121,n2)-pow(hint4,202020,n2)*pow(2020,202020*212121,n2))
p2 = n2//q2
d2 = gmpy2.invert(e,(q2-1)*(p2-1))
q = pow(c2,d2,n2)
d1 = gmpy2.invert(e,(q1-1)*(p1-1))
p = pow(c1,d1,n1)
d = gmpy2.invert(e,(q-1)*(p-1))
m = pow(c,d,p*q)
print(long_to_bytes(m))

2022 *ctf crypto Ezrsa

这题严格来说是需要用到coppersmith里的内容，不过也是进行了改编，必须求出一部分条件再来求解

from Crypto.Util.number import getStrongPrime
from gmpy import next_prime
from random import getrandbits
from flag import flag
p=getStrongPrime(1024)
q=next_prime(p^((1<<900)-1)^getrandbits(300))
n=p*q
e=65537
m=int(flag.encode('hex'),16)
assert m<n
c=pow(m,e,n)
print(hex(n))
#0xe78ab40c343d4985c1de167e80ba2657c7ee8c2e26d88e0026b68fe400224a3bd7e2a7103c3b01ea4d171f5cf68c8f00a64304630e07341cde0bc74ef5c88dcbb9822765df53182e3f57153b5f93ff857d496c6561c3ddbe0ce6ff64ba11d4edfc18a0350c3d0e1f8bd11b3560a111d3a3178ed4a28579c4f1e0dc17cb02c3ac38a66a230ba9a2f741f9168641c8ce28a3a8c33d523553864f014752a04737e555213f253a72f158893f80e631de2f55d1d0b2b654fc7fa4d5b3d95617e8253573967de68f6178f78bb7c4788a3a1e9778cbfc7c7fa8beffe24276b9ad85b11eed01b872b74cdc44959059c67c18b0b7a1d57512319a5e84a9a0735fa536f1b3
print(hex(c))
#0xd7f6c90512bc9494370c3955ff3136bb245a6d1095e43d8636f66f11db525f2063b14b2a4363a96e6eb1bea1e9b2cc62b0cae7659f18f2b8e41fca557281a1e859e8e6b35bd114655b6bf5e454753653309a794fa52ff2e79433ca4bbeb1ab9a78ec49f49ebee2636abd9dd9b80306ae1b87a86c8012211bda88e6e14c58805feb6721a01481d1a7031eb3333375a81858ff3b58d8837c188ffcb982a631e1a7a603b947a6984bd78516c71cfc737aaba479688d56df2c0952deaf496a4eb3f603a46a90efbe9e82a6aef8cfb23e5fcb938c9049b227b7f15c878bd99b61b6c56db7dfff43cd457429d5dcdb5fe314f1cdf317d0c5202bad6a9770076e9b25b1

题目所给出的信息只有n和c,那就只能在p,q的关系上下手了
p是一个强素数
q根据p来生成一个素数

q=next_prime(p^((1<<900)-1)^getrandbits(300))

直观看就是

( p^q ) = 1<<600 - 1

然并卵，根据最后的随机位数是300,小于512，是可以利用p高位攻击的，所以可以判断出我们至少要求出一个p的前面512位，就行了

自己生成了一些随机数据，发现开根号后，p,q前面122到124是一样的，然后大胆判断前面是124位是一样的，这样只剩900位，符合出题的思路。
然后就宕机了
先说官方wp，确定了之前的124位后，然后一位一位判断过去，不断逼近n的大小，因为现在我们的p是124位高位+900个1，q是124高位+900个0，可以肯定的是，在900到300这之间是的位p,q是一个1，一个0，然后就开始对每一位进行判断，如果异或后的p*q>n,那肯定不对，差的这一步是没想到0，1的位置的影响这么大，变成只有大于n和小于n的俩种情况，之后一步步判断就可以了，根据p的高位攻击的要求，只要有512位就可以了，所以最后的判断应该是有偏差的，但只要保证高位准确即可。

from Crypto.Util.number import *
n=0xe78ab40c343d4985c1de167e80ba2657c7ee8c2e26d88e0026b68fe400224a3bd7e2a7103c3b01ea4d171f5cf68c8f00a64304630e07341cde0bc74ef5c88dcbb9822765df53182e3f57153b5f93ff857d496c6561c3ddbe0ce6ff64ba11d4edfc18a0350c3d0e1f8bd11b3560a111d3a3178ed4a28579c4f1e0dc17cb02c3ac38a66a230ba9a2f741f9168641c8ce28a3a8c33d523553864f014752a04737e555213f253a72f158893f80e631de2f55d1d0b2b654fc7fa4d5b3d95617e8253573967de68f6178f78bb7c4788a3a1e9778cbfc7c7fa8beffe24276b9ad85b11eed01b872b74cdc44959059c67c18b0b7a1d57512319a5e84a9a0735fa536f1b3
c=0xd7f6c90512bc9494370c3955ff3136bb245a6d1095e43d8636f66f11db525f2063b14b2a4363a96e6eb1bea1e9b2cc62b0cae7659f18f2b8e41fca557281a1e859e8e6b35bd114655b6bf5e454753653309a794fa52ff2e79433ca4bbeb1ab9a78ec49f49ebee2636abd9dd9b80306ae1b87a86c8012211bda88e6e14c58805feb6721a01481d1a7031eb3333375a81858ff3b58d8837c188ffcb982a631e1a7a603b947a6984bd78516c71cfc737aaba479688d56df2c0952deaf496a4eb3f603a46a90efbe9e82a6aef8cfb23e5fcb938c9049b227b7f15c878bd99b61b6c56db7dfff43cd457429d5dcdb5fe314f1cdf317d0c5202bad6a9770076e9b25b1
p = (1<<900)-(1<<300)
q = 1<<300-1  
PR.<x> = PolynomialRing(Zmod(n))
pm=int(sqrt(n))>>900
p = (1<<900)-1
p+=pm*(1<<900)
q+=pm*(1<<900)   #这俩步设置p高124位相同
#in the rest place, '1' either belong to p or q
for i in range(898, 301, -1):#这里也可以900--450只要保证最后解出来的有512位以上的高位即可
cur = 1<<i
if (p^^cur) * (q^^cur) < n:#sage中^^是异或，^是次方，与python中相同
p ^^= cur
q ^^= cur
f=x+p
roots=f.small_roots(X=2**450,beta=0.4) #这里根据你解出的明文数确定，# beta=0.4表明存在factor 大于n ^0.4，这里小了会报错，只能是0.4，这跟位数也有关系，需要设计
p=p+roots[0]
q=n//int(p)
fn=(p-1)*(q-1)
d=inverse(65537,fn)
print(hex(int(pow(c,d,n)))[2:-1].decode('hex'))

接下来分析一下Nu1L的wp
主要还是看生成p高位部分的

s = ((int(n**(1/2))>>899)+1)<<900
l = 0 
r = int(n**(1/2))
while r-l>1: 
m = (l+r)>>1
if (m+n/m)>s: 
l = m
else:
r = m

这里s是简写了一些操作，不过他表示的意思是p+q
然后之后就不断找这个值
刚开始的m是比较小的，要提升l，并且此时的p+q也是会比s要大的,后续就是一样的

羊城杯 2020 RRRRRRRSA

RSA连分数求解
先列出rsa中的密钥的式子

可以发现当p,q很大时,phi和n是接近的,1/(dphi)很小,说明e/phi 和k/d 很接近,这里phi可以近似看成n. 于是e/n 和k/d 很接近. 当e很大时,通过对e/n进行连分数展开,然后对每一项求其渐进分数,通过遍历渐进分数，k/d很有可能就被e/n的众多项渐进分数中的一项所覆盖, 假设覆盖它的是k1/d1,那么k1=k ; d1=d.这里可能会有疑问,如果gcd(k,d)!=1 那么对于最简的k1/d1来说是否应该存在t使得tk1=k td1=d 呢? 但其实这里 gcd(k,d)一定为1即k,d一定互质.证明也很简单.前面我们可以得到: ed-kphi=1 对于这么一个式子,在扩展欧几里得里有如果gcd(d,k)!=1 那么该该方程无解.(不互质可以提出一个不为1公因子,除过去左边全是整数而右边却是真分数显然不可能) 其实连分数的运用不仅限于此，只要你先求出如下形式的俩个k1,k2，就可以尝试使用连分数

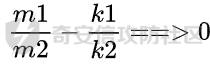
条件是m1,m2已知，并且要用终止条件
先看题目

from Crypto.Util.number import *
from secret import flag
import random
m1 = bytes_to_long(flag[:len(flag) // 2])
m2 = bytes_to_long(flag[len(flag) // 2:])
def gen(pbits, qbits):
p1, q1 = getPrime(pbits), getPrime(qbits)
n1 = p1**4*q1
q2 = getPrime(qbits)
bound = p1 // (8*q1*q2) + 1
p2 = random.randrange(p1, p1 + bound)
while not isPrime(p2):
p2 = random.randrange(p1, p1 + bound)
n2 = p2**4*q2
return (n1, n2), (p1, q1), (p2, q2)
e = 0x10001
pbits = int(360)
qbits = int(128)
pk, sk1, sk2 = gen(pbits, qbits)
c1 = pow(m1, e, pk[0])
c2 = pow(m2, e, pk[1])
print(f'pk = {pk}')
print(f'c1, c2 = {c1, c2}')
"""
pk = (1150398070565459492080597718626032792435556703413923483458704675295997646493249759818468321328556510074044954676615760446708253531839417036997811506222349194302791943489195718713797322878586379546657275419261647635859989280700191441312691274285176619391539387875252135478424580680264554294179123254566796890998243909286508189826458854346825493157697201495100628216832191035903848391447704849808577310612723700318670466035077202673373956324725108350230357879374234418393233, 1242678737076048096780023147702514112272319497423818488193557934695583793070332178723043194823444815153743889740338870676093799728875725651036060313223096288606947708155579060628807516053981975820338028456770109640111153719903207363617099371353910243497871090334898522942934052035102902892149792570965804205461900841595290667647854346905445201396273291648968142608158533514391348407631818144116768794595226974831093526512117505486679153727123796834305088741279455621586989)
c1, c2 = (361624030197288323178211941746074961985876772079713896964822566468795093475887773853629454653096485450671233584616088768705417987527877166166213574572987732852155320225332020636386698169212072312758052524652761304795529199864805108000796457423822443871436659548626629448170698048984709740274043050729249408577243328282313593461300703078854044587993248807613713896590402657788194264718603549894361488507629356532718775278399264279359256975688280723740017979438505001819438, 33322989148902718763644384246610630825314206644879155585369541624158380990667828419255828083639294898100922608833810585530801931417726134558845725168047585271855248605561256531342703212030641555260907310067120102069499927711242804407691706542428236208695153618955781372741765233319988193384708525251620506966304554054884590718068210659709406626033891748214407992041364462525367373648910810036622684929049996166651416565651803952838857960054689875755131784246099270581394)
"""

我们知道n1,n2
列下式子

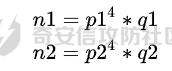
俩个相除

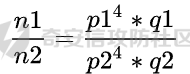
显然我们可以知道的是N1/N2 <p1/p2 ; N1/N2<q1/q2 所以在q1/q2在区间(N1/N2,1)之间. 尝试对N1/N2进行连分数展开并求其各项渐进分数,记为ti/si并验证N1%ti==0是否成立,如果成立,那么return

import gmpy2
N1=1150398070565459492080597718626032792435556703413923483458704675295997646493249759818468321328556510074044954676615760446708253531839417036997811506222349194302791943489195718713797322878586379546657275419261647635859989280700191441312691274285176619391539387875252135478424580680264554294179123254566796890998243909286508189826458854346825493157697201495100628216832191035903848391447704849808577310612723700318670466035077202673373956324725108350230357879374234418393233
c1=361624030197288323178211941746074961985876772079713896964822566468795093475887773853629454653096485450671233584616088768705417987527877166166213574572987732852155320225332020636386698169212072312758052524652761304795529199864805108000796457423822443871436659548626629448170698048984709740274043050729249408577243328282313593461300703078854044587993248807613713896590402657788194264718603549894361488507629356532718775278399264279359256975688280723740017979438505001819438
E1=0x10001
N2=1242678737076048096780023147702514112272319497423818488193557934695583793070332178723043194823444815153743889740338870676093799728875725651036060313223096288606947708155579060628807516053981975820338028456770109640111153719903207363617099371353910243497871090334898522942934052035102902892149792570965804205461900841595290667647854346905445201396273291648968142608158533514391348407631818144116768794595226974831093526512117505486679153727123796834305088741279455621586989
c2=33322989148902718763644384246610630825314206644879155585369541624158380990667828419255828083639294898100922608833810585530801931417726134558845725168047585271855248605561256531342703212030641555260907310067120102069499927711242804407691706542428236208695153618955781372741765233319988193384708525251620506966304554054884590718068210659709406626033891748214407992041364462525367373648910810036622684929049996166651416565651803952838857960054689875755131784246099270581394
E2=0x10001
def continuedFra(x, y):
cF = []
while y:
cF += [x // y]
x, y = y, x % y
return cF
def Simplify(ctnf):
numerator = 0
denominator = 1
for x in ctnf[::-1]:
numerator, denominator = denominator, x * denominator + numerator
return (numerator, denominator)
def getit(c):
cf=[]
for i in range(1,len(c)):
cf.append(Simplify(c[:i]))
return cf
#求渐进分数
def wienerAttack(e, n):
cf=continuedFra(e,n)
for (p2,p1) in getit(cf):
if p1 == 0:
continue
if N1%p1==0 and p1!=1:
return p1,p2
print('not find!')
q1,q2 = wienerAttack(N1,N2)
p1 = gmpy2.iroot(N1//q1,4)[0]
p2 = gmpy2.iroot(N2//q2,4)[0]
phi1=p1**3*(p1-1)*(q1-1)
phi2=p2**3*(p2-1)*(q2-1)
d1=gmpy2.invert(E1,phi1)
d2=gmpy2.invert(E2,phi2)
from Crypto.Util import number
m1=number.long_to_bytes(gmpy2.powmod(c1,d1,N1))
m2=number.long_to_bytes(gmpy2.powmod(c2,d2,N2))
print((m1+m2))

2022 zer0pts CTF Anti-Fermat

from Crypto.Util.number import isPrime, getStrongPrime
from gmpy import next_prime
from secret import flag
# Anti-Fermat Key Generation
p = getStrongPrime(1024)
q = next_prime(p ^ ((1<<1024)-1))
n = p * q
e = 65537
# Encryption
m = int.from_bytes(flag, 'big')
assert m < n
c = pow(m, e, n)
print('n = {}'.format(hex(n)))
print('c = {}'.format(hex(c)))
#n = 0x1ffc7dc6b9667b0dcd00d6ae92fb34ed0f3d84285364c73fbf6a572c9081931be0b0610464152de7e0468ca7452c738611656f1f9217a944e64ca2b3a89d889ffc06e6503cfec3ccb491e9b6176ec468687bf4763c6591f89e750bf1e4f9d6855752c19de4289d1a7cea33b077bdcda3c84f6f3762dc9d96d2853f94cc688b3c9d8e67386a147524a2b23b1092f0be1aa286f2aa13aafba62604435acbaa79f4e53dea93ae8a22655287f4d2fa95269877991c57da6fdeeb3d46270cd69b6bfa537bfd14c926cf39b94d0f06228313d21ec6be2311f526e6515069dbb1b06fe3cf1f62c0962da2bc98fa4808c201e4efe7a252f9f823e710d6ad2fb974949751
#c = 0x60160bfed79384048d0d46b807322e65c037fa90fac9fd08b512a3931b6dca2a745443a9b90de2fa47aaf8a250287e34563e6b1a6761dc0ccb99cb9d67ae1c9f49699651eafb71a74b097fc0def77cf287010f1e7bd614dccfb411cdccbb84c60830e515c05481769bd95e656d839337d430db66abcd3a869c6348616b78d06eb903f8abd121c851696bd4cb2a1a40a07eea17c4e33c6a1beafb79d881d595472ab6ce3c61d6d62c4ef6fa8903149435c844a3fab9286d212da72b2548f087e37105f4657d5a946afd12b1822ceb99c3b407bb40e21163c1466d116d67c16a2a3a79e5cc9d1f6a1054d6be6731e3cd19abbd9e9b23309f87bfe51a822410a62

存在以下关系

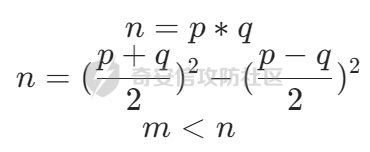
这里通过观察，可以有以下发现
p - (q^((1<<1024)-1)) - 1
和
p + q - (1<<1024)
是相一样的并且值比较很小
此时可以写出类似的式子

带入之前的n的平方差公式里有

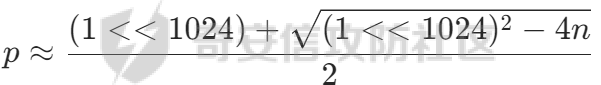
这样算出来还只是个近似值，需要使用nextprime进行判断

from Crypto.Util.number import *
import gmpy2
import sympy
n = int(0x1ffc7dc6b9667b0dcd00d6ae92fb34ed0f3d84285364c73fbf6a572c9081931be0b0610464152de7e0468ca7452c738611656f1f9217a944e64ca2b3a89d889ffc06e6503cfec3ccb491e9b6176ec468687bf4763c6591f89e750bf1e4f9d6855752c19de4289d1a7cea33b077bdcda3c84f6f3762dc9d96d2853f94cc688b3c9d8e67386a147524a2b23b1092f0be1aa286f2aa13aafba62604435acbaa79f4e53dea93ae8a22655287f4d2fa95269877991c57da6fdeeb3d46270cd69b6bfa537bfd14c926cf39b94d0f06228313d21ec6be2311f526e6515069dbb1b06fe3cf1f62c0962da2bc98fa4808c201e4efe7a252f9f823e710d6ad2fb974949751)
c = int(0x60160bfed79384048d0d46b807322e65c037fa90fac9fd08b512a3931b6dca2a745443a9b90de2fa47aaf8a250287e34563e6b1a6761dc0ccb99cb9d67ae1c9f49699651eafb71a74b097fc0def77cf287010f1e7bd614dccfb411cdccbb84c60830e515c05481769bd95e656d839337d430db66abcd3a869c6348616b78d06eb903f8abd121c851696bd4cb2a1a40a07eea17c4e33c6a1beafb79d881d595472ab6ce3c61d6d62c4ef6fa8903149435c844a3fab9286d212da72b2548f087e37105f4657d5a946afd12b1822ceb99c3b407bb40e21163c1466d116d67c16a2a3a79e5cc9d1f6a1054d6be6731e3cd19abbd9e9b23309f87bfe51a822410a62)
e = 65537
p=(gmpy2.iroot(pow(2,2048)-4*n,2)[0]+pow(2,1024))//2
p=int(p)
while(1):
p=sympy.nextprime(p)
if(n%p==0):
print(p)
break
q=n//p
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,n)
flag=long_to_bytes(int(m))
print(flag)

这些题只是一部分，不过其中的漏洞都需要去仔细分析验证才能得到最后的结论和破解的方法